Serie harmónica
En matemáticas, a serie harmónica é a serie infinita formada pola suma de todas as fraccións unitarias positivas:
Os primeiros termos da serie suman aproximadamente , onde é o logaritmo natural e é a constante de Euler-Mascheroni. Como o logaritmo ten valores arbitrariamente grandes, a serie harmónica non ten un límite finito: é unha serie diverxente. A súa diverxencia foi probada no século XIV por Nicole Oresme utilizando un precursor da proba de condensación de Cauchy para a converxencia de series infinitas. Tamén se pode demostrar que diverxe comparando a suma cunha integral, segundo a proba de converxencia da integral.
Definición e diverxencia
A serie harmónica é a serie infinita
- na que os termos son todas as fraccións unitarias positivas. É unha serie diverxente: a medida que se inclúen máis termos da serie nas sumas parciais da serie, os valores destas sumas parciais medran arbitrariamente, máis aló de calquera límite finito. Debido a que é unha serie diverxente, debería interpretarse como unha suma formal, unha expresión matemática abstracta que combina as fraccións unitarias, máis que como algo que se pode avaliar a un valor numérico. Hai moitas probas diferentes da diverxencia da serie harmónica, analizadas nun artigo de 2006 por SJ Kifowit e TA Stamps.[1] Dúas das [2] Modelo:R máis coñecidas están listadas a continuación.
Proba por comparación
Unha forma de probar a diverxencia é comparar a serie harmónica con outra serie diverxente, onde cada denominador é substituído pola seguinte potencia de dous:
- A agrupación de termos iguais mostra que a segunda serie diverxe (porque é unha suma infinita de cantidades 1/2):
- Debido a que cada termo da serie harmónica é maior ou igual ao termo correspondente da segunda serie (e os termos son todos positivos), e dado que a segunda serie diverxe, dedúcese (polo test de comparación) que a serie harmónica tamén diverxe. O mesmo argumento demostra con máis forza que, para todo enteiro positivo ,
Esta é a proba orixinal dada por Nicole Oresme en torno a 1350.Modelo:R A proba de condensación de Cauchy é unha xeneralización deste argumento.[3]
Proba por comparación cunha integral

É posíbel demostrar que a serie harmónica diverxe comparando a súa suma cunha integral impropia. Concretamente, considere a disposición dos rectángulos que se mostra na figura da dereita. Cada rectángulo ten 1 unidade de ancho e unidades altas, polo que se a serie harmónica converxe, a área total dos rectángulos sería a suma das series harmónicas. A curva permanece totalmente por debaixo do límite superior dos rectángulos, polo que a área baixo a curva (no rango de do un ao infinito que está cuberto por rectángulos) sería menor que a área de unión dos rectángulos. No entanto, a área baixo a curva vén dada por unha integral impropia diverxente,
- Como esta integral non converxe, a suma tampouco non pode converxer. Modelo:R
Sumas parciais
Sumando os primeiros termos da serie harmónica temos unha suma parcial chamada número harmónico e denotado como :[4]
| Valor de n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Valor aprox. de | 1 | 1,5 | 1,8 | 2,1 | 2,3 | 2,5 | 2,6 | 2,7 | 2,8 | 2,9 | 3,0 | 3,1 | 3,2 | 3,25 | 3,32 | 3,38 | 3,44 | 3,49 | 3,55 | 3,60 |
De feito, a serie harmónica diverxe, as súas sumas parciais tenden cara a Modelo:Math.
| Valor de n | 10 | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Valor aprox. de | 2,9 | 5,2 | 7,5 | 9,8 | 12,1 | 14,4 | 16,7 | 19,0 | 21,3 |
Taxa de crecemento
Estes números medran moi lentamente, cun crecemento logarítmico, como se pode ver na proba da integral.[5] Máis precisamente, pola fórmula de Euler-Maclaurin,
- onde é a constante de Euler-Mascheroni e que se achega a 0 cando vai ao infinito.
Interpolación
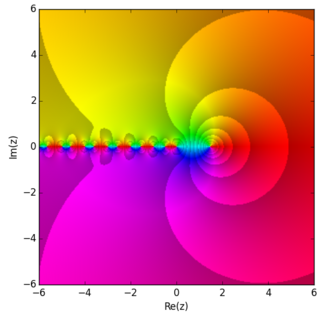
A función digamma defínese como a derivada logarítmica da función gamma
- Así como a función gamma proporciona unha interpolación continua dos factoriais, a función digamma proporciona unha interpolación continua dos números harmónicos, no sentido de que .[6] Esta ecuación pódese usar para estender a definición a números harmónicos con índices racionais.[7]
Series relacionadas
Serie harmónica alternada
A serie
- coñécese como serie harmónica alternada. É condicionalmente converxente polo test de serie alternada, pero non é absolutamente converxente. A súa suma é o logaritmo neperiano de 2.[8]
A expansión asintótica da serie comeza como
- Isto resulta da igualdade e a fórmula de Euler-Maclaurin.
Función zeta de Riemann
A función zeta de Riemann defínese para real pola serie converxente
- que para sería a serie harmónica. Pódese estender mediante o prolongamento analítico a unha función holomorfa en todos os números complexos agás Modelo:Nowrap onde a función estendida ten un polo simple. Outros valores importantes da función zeta inclúen Modelo:Nowrap que é a solución ao problema de Basilea, a constante de Apéry Modelo:Nowrap que Roger Apéry demostrou que é un número irracional, e a "liña crítica" dos números complexos con parte real Modelo:Nowrap conxecturado pola hipótese de Riemann como os únicos valores distintos dos enteiros negativos onde a función pode ser cero.[9]
Notas
Véxase tamén
Bibliografía
- Modelo:Cita publicación periódica ver problema 52: De homine patrefamilias – A lord of the manor, pp. 124–125.
- Modelo:Cita libro
From p. 250, prop. 16: "XVI. Summa serei infinita harmonicè progressionalium,
- Modelo:Cita libro proba de Johann Bernoulli tamén por contradición.
- Modelo:Cita publicación periódica See also unpublished addendum, "More proofs of divergence of the harmonic series" por Kifowit.
- Modelo:Cita libro A proba de Mengoli é por contradición
- Modelo:Cita publicación periódica ver en particular Teorema 1, p. 516.
- Modelo:Cita publicación periódica
- Modelo:Cita publicación periódica
- Modelo:Cita publicación periódica