Número pi

	Números – Números irracionais ; ζ(3) – 2 – 3 – 5 – ϕ – α – e – π – δ
Binario	11,00100100001111110110…
Decimal	3,14159265358979323846…
Hexadecimal	3,243F6A8885A308D31319…
Fracción continua	3+17+115+11+1292+⋱; Nótese que esta fracción continua non é periódica.

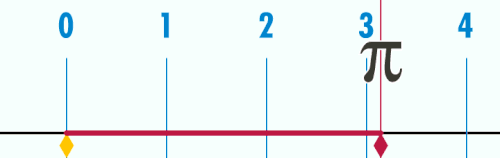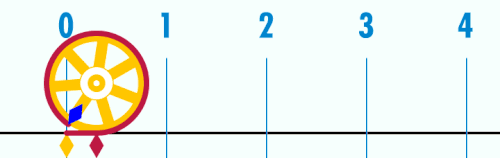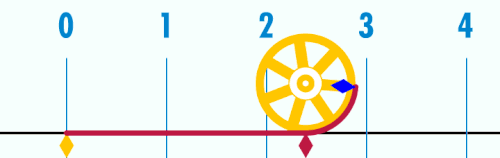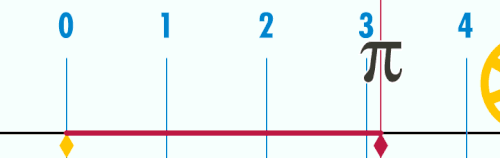
Modelo:1000 Modelo:1000 artigos icona título Modelo:Outros homónimos

Cando o diámetro dun círculo é 1, a lonxitude da circunferencia é pi.

Pi ou π é unha constante matemática cuxo valor é a razón aritmética de calquera circunferencia dun círculo co seu diámetro; este é o mesmo valor có da razón da área dun círculo co cadrado do seu raio. É aproximadamente igual a 3,14159 na notación decimal habitual. π é unha das constantes matemáticas e físicas máis importantes: moitas fórmulas das matemáticas, ciencias e enxeñaría están moi relacionadas con π^[1].

π é un número irracional, o que significa que o seu valor non pode ser expresado exactamente como fracción m/n, onde m e n son enteiros. Por conseguinte, a súa representación decimal nunca acaba ou se repite. É tamén un número transcendente, o que quere dicir que non existen secuencias finitas de operacións alxébricas con números enteiros (multiplicacións, raíces, sumas etc.) que poidan ser igual ao seu valor; demostrar isto foi un logro recente na historia das matemáticas e un resultado significativo das matemáticas alemás do século XIX. Ao longo da historia matemática, teñen habido moitos esforzos por determinar π máis exactamente e entender a súa natureza; a fascinación co número mesmo pasou á cultura non-matemática.

A letra grega π, frecuentemente enunciada pi, foi adoptada para o número a partir da palabra grega para perímetro "περίμετρος", por vez primeira por William Jones en 1707, e popularizada por Leonhard Euler en 1737^[2]. A constante tamén é ocasionalmente referida coma a "constante circular", a "constante de Arquímedes" (para non ser confundida co número de Arquímedes) ou "número de Ludolph" (na honra dun matemático alemán cuxos esforzos para calcular os máis dos seus díxitos fixérono coñecido).

Definicións

En xeometría plana, π pódese definir como a relación da circunferencia co seu diámetro.
Tamén se define π analiticamente usando funcións trigonométricas, como exemplos:
- como o menor positivo x para o cal sen(x) = 0,
- como o duplo do menor positivo x para o cal cos(x) = 0.

A probabilidade e o número π

Unha lixeira reflexión pode facernos pensar que nada hai máis afastado do número π que o concepto de probabilidade, cando a realidade é ben distinta. O matemático e lóxico inglés Augustus De Morgan foi interrogado en certa ocasión por un vendedor de seguros sobre a probabilidade de que un grupo de persoas seguise con vida despois dun certo tempo. Na solución ao problema aparecía o número π, cousa que sorprendeu ao vendedor quen pensou que De Morgan se trabucara. A solución era a correcta e ten que ver coa distribución normal, unha variable aleatoria continua cuxa función de densidade é:

f (x) = \frac{1}{σ \sqrt{2 π}} e^{- \frac{(x - μ)^{2}}{2 σ^{2}}}

onde μ é a media e σ a desviación típica da distribución.

A distribución normal aparece ligada a multitude de situacións reais, entre elas á esperanza de vida do problema do vendedor de seguros. A gráfica desta distribución coñécese como campá de Gauss pola súa forma característica de campá e polo matemático alemán Gauss, quen en 1809 publicou un monográfico no que introducía algúns conceptos estatísticos, entre eles o de distribución normal; porén algúns autores atribúenlle o descubrimento en 1733 ao matemático francés Abraham de Moivre, estudando os coeficientes do binomio Modelo:Nowrap. É por este nome que Alexander Pope dicía que cada vez que alguén morre, as campás (de Gauss) soan por π.

Outros exemplos do campo das probabilidades onde aparece π son:

A probabilidade de que dous enteiros positivos escollidos ó chou sexan primos entre si é $6 / π^{2}$
Elixido ó chou un triángulo cuxo lado maior mide a unidade, a probabilidade de que sexa obtusángulo é $(π - 2) / 4$
O problema da agulla de Buffon: chamado así por ser proposto, e resolto, polo conde de Buffon, científico francés do século XVIII. Lanzada unha agulla, sen que se clave, sobre unha superficie na que se trazaron liñas paralelas equidistantes, trátase de calcular a probabilidade de que a agulla corte a unha liña. Se $l$ é a lonxitude da agulla, e $d$ a distancia entre as liñas, dita probabilidade é:

$\frac{2 l}{π d}$ cando $l < d$
$\frac{2}{π}$ cando $l = d$
$\frac{2 l}{π d} - \frac{2}{π d} {\sqrt{l^{2} - d^{2}} + d \sin^{- 1} (\frac{d}{l})} + 1$ cando $l > d$

O problema da agulla de Buffon-Laplace: foi proposto por Laplace en 1812. É unha variante do problema de Buffon considerando a superficie cuadriculada onde os lados da cuadrícula $a$ e $b$ non teñen por que medir o mesmo, e a lonxitude da agulla $l$ é menor que ambos lados.

Se $a \neq b$ , a probabilidade de que a agulla corte a algún lado da cuadrícula é: $\frac{2 l (a + b) - l^{2}}{π a b}$
Se $a = b$ , téñense as seguintes probabilidades:

Probabilidade de que a agulla non corte a ningunha liña: $1 - \frac{l (4 a - l)}{π a^{2}}$
Probabilidade de que a agulla corte a unha liña: $\frac{2 l (2 a - l)}{π a^{2}}$
Probabilidade de que a agulla corte ás dúas liñas: $\frac{l^{2}}{π a^{2}}$

A suma das tres probabilidades anteriores é obviamente 1 xa que abarcan todas as posibilidades e corresponden a sucesos incompatíbeis.

Fórmulas que conteñen π

Xeometría

Ángulos: 180 graos son equivalentes a π radiáns

Forma xeométrica	Fórmula
Circunferencia do círculo de raio r e diámetro d	$C = π d = 2 π r$
Área do círculo de raio r	$A = π r^{2}$
Área da elipse con semi-eixos a e mais b	$A = π a b$
Volume da esfera de raio r	$V = \frac{4}{3} π r^{3}$
Superficie da esfera de raio r	$A = 4 π r^{2}$
Volume do cilindro de altura h e raio r	$V = π r^{2} h$
Superficie do cilindro de altura h e raio r	$A = 2 (π r^{2}) + (2 π r) h = 2 π r (r + h)$
Volume do cono de altura h e raio r	$V = \frac{1}{3} π r^{2} h$
Superficie do cono de altura h e raio r	$A = π r \sqrt{r^{2} + h^{2}} + π r^{2} = π r (r + \sqrt{r^{2} + h^{2}})$

Ademais, o ángulo 180° en graos equivale a π radiáns (unha volta enteira, 360 graos, son equivalentes a 2π radiáns).

Análise

Moitas fórmulas de análise matemática conteñen π, incluíndo series infinitas, integrais, e as chamadas funcións especiais.

François Viète, 1593 (Proba de Viète):

\frac{2}{π} = \frac{\sqrt{2}}{2} \frac{\sqrt{2 + \sqrt{2}}}{2} \frac{\sqrt{2 + \sqrt{2 + \sqrt{2}}}}{2} \dots

fórmula de Leibniz:

\frac{1}{1} - \frac{1}{3} + \frac{1}{5} - \frac{1}{7} + \frac{1}{9} - \dots = \frac{π}{4}

Esta serie infinita, citada a miúdo, escríbese como se indica arriba, pero exprésase máis tecnicamente como:

\sum_{n = 0}^{\infty} (- 1)^{n} (\frac{1}{2 n + 1}) = \frac{π}{4}

produto de Wallis (ver este artigo para a proba):

\frac{2}{1} \cdot \frac{2}{3} \cdot \frac{4}{3} \cdot \frac{4}{5} \cdot \frac{6}{5} \cdot \frac{6}{7} \cdot \frac{8}{7} \cdot \frac{8}{9} \dots = \frac{π}{2}

Unha fórmula de cálculo integral :

\int_{- \infty}^{\infty} e^{- x^{2}} d x = \sqrt{π}

problema de Basilea, resolta por Euler (ver tamén función zeta de Riemann ):

ζ (2) = \frac{1}{1^{2}} + \frac{1}{2^{2}} + \frac{1}{3^{2}} + \frac{1}{4^{2}} + \dots = \frac{π^{2}}{6}

ζ (4) = \frac{1}{1^{4}} + \frac{1}{2^{4}} + \frac{1}{3^{4}} + \frac{1}{4^{4}} + \dots = \frac{π^{4}}{90}

e xeralmente,

ζ (2 n)

é un múltiplo de

π^{2 n}

para o enteiro positivo n

función gamma avaliada en 1/2:

Γ (\frac{1}{2}) = \sqrt{π}

aproximación de Stirling:

n! \sim \sqrt{2 π n} {(\frac{n}{e})}^{n}

identidade de Euler (chamada por Richard Feynman "a fórmula máis salientada en matemáticas"):

e^{i π} + 1 = 0

Area dun cuarto do círculo unidade:

\int_{0}^{1} \sqrt{1 - x^{2}} d x = \frac{π}{4}

Historia

Antigüidade

As aproximacións máis coñecidas a π datan de antes da nosa era e tiñan unha precisión de dúas cifras decimais; esta precisión mellorouse, sobre todo nas matemáticas chinesas en particular a mediados do primeiro milenio, ata unha precisión de sete cifras decimais. A partir de entón, non se produciron máis avances ata finais da Idade Media.

As primeiras aproximacións escritas de π atópanse en Babilonia e Exipto, ambas dentro do un por cento do valor verdadeiro. En Babilonia, unha tableta de arxila datada entre 1900 e 1600 a.C. ten un enunciado xeométrico que, implicitamente, trata a π como Modelo:Sfrac = 3.125.Modelo:Sfn En Exipto, o papiro de Rhind, datado ao redor de 1650 AC pero copiado dun documento datado en 1850 AC, ten unha fórmula para a área dun círculo que trata a π como Modelo:Nowrap 3.16.^[3]Modelo:Sfn Aínda que algúns piramidólogos como Flinders Petrie han teorizado que a Gran Pirámide de Gizeh foi construída con proporcións relacionadas con π, esta teoría non é amplamente aceptada polos estudosos.^[4] Nos textos Shulba Sutras das matemáticas indias, que datan dunha tradición oral do primeiro ou segundo milenio a.C., danse aproximacións que foron interpretadas de diversas maneiras como aproximadamente 3.08831, 3.08833, 3.004, 3, ou 3.125.^[5]

Era de aproximación de polígonos

O primeiro algoritmo rexistrado para calcular rigorosamente o valor de π foi un enfoque xeométrico mediante polígonos, ideado ao redor do 250 a.C. polo matemático grego Arquímedes.Modelo:Sfn Este algoritmo poligonal dominou durante máis de 1.000 anos, e como resultado π coñécese ás veces como a constante de Arquímedes.Modelo:Sfn Arquímedes calculou os límites superior e inferior de π debuxando un hexágono regular dentro e fóra dun círculo, e duplicando sucesivamente o número de lados ata chegar a un polígono regular de 96 lados. Ao calcular os perímetros destes polígonos, demostrou que Modelo:Math (é dicir Modelo:Math).^[6] O límite superior de Arquímedes de Modelo:Math puido levar a unha crenza popular estendida de que π é igual a Modelo:Math.Modelo:Sfn Ao redor do 150 d. C., o científico grego-romano Tolomeo, no seu Almaxesto, deu un valor para π de 3,1416, que puido ter obtido de Arquímedes ou de Apolonio de Perge.Modelo:Sfn Modelo:Sfn Os matemáticos que usaban algoritmos poligonais alcanzaron os 39 díxitos de π en 1630, un récord que só se bateu en 1699 cando se usaron series infinitas para acadar os 71 díxitos.^[7]

Na China antiga, os valores de π eran 3,1547 (ao redor do ano 1 d. C.), √10 (aproximadamente 3.1623 no 100 d.C.), e Modelo:Math ( aproximadamente 3,1556 no século III).Modelo:Sfn Ao redor do 265 d. C., o matemático do reino Wei Li Hui creou un algoritmo iterativo baseado en polígonos e utilizouno cun polígono de 3.072 lados para obter un valor. de π de 3.1416.^[8]Modelo:Sfn Liu máis tarde inventou un método máis rápido para calcular π e obtivo un valor de 3,14 cun polígono de 96 lados, aproveitando que as diferenzas na área dos sucesivos polígonos forman unha serie xeométrica cun factor de 4.^[8] O matemático chinés Zu Chongzhi, ao redor do ano 480 d. C., calculou que Modelo:Math e suxeriu as aproximacións Modelo:Math = 3.14159292035... e Modelo:Math = 3.142857142857..., que chamou Milü (''proporción proxima") e Yuelü ("proporción aproximada"), respectivamente, utilizando o algoritmo de Li Hui aplicado a un polígono de 12.288 lados. Cun valor correcto para os seus sete primeiros díxitos decimais, este valor seguiu sendo a aproximación máis exacta de π dispoñible durante os seguintes 800 anos.Modelo:Sfn

O astrónomo indio Âryabhata utilizou un valor de 3,1416 na súa Āryabhaṭīya (499 d. C.)..Modelo:Sfn Fibonacci en c. 1220 calculou 3,1418 mediante un método poligonal, independente de Arquímedes.Modelo:Sfn O autor italiano Dante ao parecer empregou o valor Modelo:Math.Modelo:Sfn

O astrónomo persa Jamshīd al-Kāshī produciu 9 díxitos sexaxesimais, aproximadamente o equivalente a 16 díxitos decimais, en 1424 utilizando un polígono con 3×2²⁸ lados,^[9]^[10] que foi o récord mundial durante uns 180 anos.Modelo:Sfn O matemático francés François Viète logrou en 1579 9 díxitos cun polígono de 3×2¹⁷ lados.Modelo:Sfn O matemático flamengo Adriaan van Roomen chegou os 15 decimais en 1593.Modelo:Sfn En 1596, o matemático holandés Ludolph van Ceulen alcanzou os 20 díxitos, un rexistro que máis tarde aumentou a 35 díxitos (como resultado, π foi chamado "número ludolphiano" en Alemaña ata principios do século XX).Modelo:Sfn O científico holandés Willebrord Snel alcanzou os 34 díxitos en 1621,Modelo:Sfn e o astrónomo austríaco Christoph Grienberger chegou a 38 díxitos en 1630 usando 10⁴⁰ lados.^[11] Christiaan Huygens foi quen de chegar a 10 cifras decimais en 1654 usando un método equivalente e lixeiramente diferente á extrapolación de Richardson.^[12]^[13]

Series infinitas

O cálculo de π foi revolucionado polo desenvolvemento das técnicas de series infinitas nos séculos XVI e XVII. Unha serie infinita é a suma dos termos dunha sucesión infinita. As series infinitas permitían aos matemáticos calcular π con moita maior precisión que Arquímedes e outros que utilizaban técnicas xeométricas.^[14] Aínda que as series infinitas foron explotadas para π sobre todo por matemáticos europeos como James Gregory e Gottfried Wilhelm Leibniz, o enfoque tamén apareceu na Escola de Kerala nalgún momento dos séculos XIV ou XV.^[15]Modelo:Sfn Ao redor de 1500 d. C., unha descrición escrita dunha serie infinita que podería usarse para calcular π foi presentada en verso sánscrito no tratado astronómico Tantrasamgraha escrito polo matemático e astronomo Nilakantha Somayaji.^[15] As series preséntanse sen probas, pero as probas preséntanse nun traballo posterior, Yuktibhāṣā, de arredor de 1530 d.C. Descríbense varias series infinitas, incluíndo series para seno (que Nilakantha atribúe a Madhava de Sangamagrama), coseno e arcotanxente que agora se denominan ás veces series de Madhava. Ás veces a serie para o arcotanxente chámase serie de Gregory ou serie de Gregory-Leibniz.^[15] Madhava utilizou series infinitas para estimar π a 11 díxitos ao redor de 1400, pero ese valor foi mellorado ao redor de 1430 polo matemático persa Jamshīd al-Kāshī, utilizando un algoritmo poligonal.^[16]

En 1593, François Viète publicou o que agora se coñece como fórmula de Viète, un produto infinito (en lugar dunha suma infinita, que se utiliza máis tipicamente nos cálculos de π): Modelo:Sfn^[17]^[18]

$\frac{2}{π} = \frac{\sqrt{2}}{2} \cdot \frac{\sqrt{2 + \sqrt{2}}}{2} \cdot \frac{\sqrt{2 + \sqrt{2 + \sqrt{2}}}}{2} \dots$

En 1655, John Wallis publicou tamén un produto infinito, o que agora se coñece como produto de Wallis:Modelo:Sfn

$\frac{π}{2} = (\frac{2}{1} \cdot \frac{2}{3}) \cdot (\frac{4}{3} \cdot \frac{4}{5}) \cdot (\frac{6}{5} \cdot \frac{6}{7}) \cdot (\frac{8}{7} \cdot \frac{8}{9}) \dots$

Un retrato formal dun home, con cabelos longos — Isaac Newton utilizou series infinitas para calcular π ata 15 díxitos, escribindo máis tarde "avergóñame dicirlle ata cantas cifras teñen estes cálculos".^[19]

Na década de 1660, o científico inglés Isaac Newton e o matemático alemán Gottfried Wilhelm Leibniz descubriron o cálculo, que conduciu ao desenvolvemento de moitas series infinitas para achegarse a π. O propio Newton utilizou unha serie arcoseno para calcular unha aproximación de 15 díxitos de π en 1665 ou 1666, escribindo "Avergóñame dicirche ata cantas cifras levei estes cálculos, non tendo outro asunto nese momento."^[19]

En 1671, James Gregory , e independentemente Leibniz en 1673, descubriron a expansión da serie de Taylor para a función de arco:^[15]^[20]^[21]

$\arctan z = z - \frac{z^{3}}{3} + \frac{z^{5}}{5} - \frac{z^{7}}{7} + \dots$

Esta serie, ás veces chamada serie de Gregory-Leibniz, é igual a Modelo:Math cando se calcula con Modelo:Math.^[21] Pero para Modelo:Math converxe de forma pouco práctica (é dicir, aproxímase á resposta moi gradualmente), necesitando unhas dez veces máis termos para calcular cada díxito adicional.

En 1699, o matemático inglés Abraham Sharp utilizou a serie de Gregory-Leibniz para $z = \frac{1}{\sqrt{3}}$ para calcular 71 díxitos de π, batendo o récord anterior de 39 díxitos, que se estableceu cun algoritmo poligonal.Modelo:Sfn

En 1706, John Machin utilizou a serie de Gregory-Leibniz para producir un algoritmo que converxía moito máis rápido:^[22]^[23]Modelo:Sfn

$\frac{π}{4} = 4 \arctan \frac{1}{5} - \arctan \frac{1}{239} .$

Machin alcanzou os 100 díxitos de π con esta fórmula.^[24] Outros matemáticos crearon variantes, agora coñecidas como fórmulas de Machin, que se utilizaron para establecer varios récords sucesivos de cálculo de díxitos de π.^[25]^[24]

Isaac Newton acelerou a converxencia da serie Gregory-Leibniz en 1684 (nun traballo inédito; outros descubriron de forma independente o mesmo resultado):^[26]

\arctan x = \frac{x}{1 + x^{2}} + \frac{2}{3} \frac{x^{3}}{(1 + x^{2})^{2}} + \frac{2 \cdot 4}{3 \cdot 5} \frac{x^{5}}{(1 + x^{2})^{3}} + \dots

Leonhard Euler popularizou esta serie no seu libro de texto de cálculo diferencial de 1755, e máis tarde utilizouna con fórmulas similares ás de Machin, incluíndo $\frac{π}{4} = 5 \arctan \frac{1}{7} + 2 \arctan \frac{3}{77},$ co que calculou 20 díxitos de π nunha hora.^[27]

As fórmulas maquinais seguiron sendo o método máis coñecido para calcular π ata ben entrada a era dos computadores, e utilizáronse para establecer récords durante 250 anos, culminando cunha aproximación de 620 díxitos en 1946 por Daniel Ferguson - a mellor aproximación lograda sen a axuda dun dispositivo de cálculo.Modelo:Sfn

En 1844, Zacharias Dase estableceu un récord, que empregou unha fórmula similar a Machin para calcular 200 decimais de π coa súa cabeza a instancias do matemático alemán Carl Friedrich Gauss.^[28]

En 1853, o matemático británico William Shanks calculou π ata os 607 díxitos, pero cometeu un erro no díxito 528, o que fixo que todos os díxitos posteriores fosen incorrectos. Aínda que en 1873 calculou 100 díxitos adicionais, co que o total ascendeu a 707, o seu erro anterior fixo que todos os novos díxitos tamén fosen incorrectos.^[29]

Taxa de converxencia

Algunhas series infinitas para $π$ converxen máis rápido que outras. Dada a elección de dúas series infinitas para π, os matemáticos xeralmente usarán a que converxa máis rapidamente porque unha converxencia máis rápida reduce a cantidade de computación necesaria para calcular $π$ con calquera precisión dada.^[30] Unha serie infinita simple para π é a Serie de Gregory-Leibniz:Modelo:Sfn

$π = \frac{4}{1} - \frac{4}{3} + \frac{4}{5} - \frac{4}{7} + \frac{4}{9} - \frac{4}{11} + \frac{4}{13} - \dots$ A medida que se engaden termos individuais desta serie infinita á suma, o total achégase gradualmente a $π$ , e cun número suficiente de termos, pode achegarse tanto a $π$ como se desexe. A converxencia é bastante lenta, aínda que, despois de 500.000 termos, só produce cinco díxitos decimais correctos de $π$ .^[31]

Unha serie infinita para $π$ (publicada por Nilakantha no século XV) que converxe máis rapidamente que a serie de Gregory-Leibniz:Modelo:Sfn^[32]

$π = 3 + \frac{4}{2 \times 3 \times 4} - \frac{4}{4 \times 5 \times 6} + \frac{4}{6 \times 7 \times 8} - \frac{4}{8 \times 9 \times 10} + \dots$ Na táboa seguinte compáranse os índices de converxencia destas dúas series:

Serie infinita para π	Despois do 1º termo	Despois do 2º termo	Despois do 3er termo	Despois do 4º termo	Despois do 5º termo	Converxe a:
$π = \frac{4}{1} - \frac{4}{3} + \frac{4}{5} - \frac{4}{7} + \frac{4}{9} - \frac{4}{11} + \frac{4}{13} + \dots$	4.0000	2.6666 ...	3.4666 ...	2.8952 ...	3.3396 ...	π = 3.1415 ...
$π = 3 + \frac{4}{2 \times 3 \times 4} - \frac{4}{4 \times 5 \times 6} + \frac{4}{6 \times 7 \times 8} - \dots$	3.0000	3.1666 ...	3.1333 ...	3.1452 ...	3.1396 ...	π = 3.1415 ...

Despois de cinco termos, a suma da serie de Gregory-Leibniz está a $0, 2$ do valor correcto de $π$ , mentres que a suma da serie de Nilakantha está a $0, 002$ do valor correcto. A serie de Nilakantha converxe máis rápido e é máis útil para calcular os díxitos de $π$ . As series que converxen aínda máis rápido inclúen as series de Machin e de Chudnovsky, este último produce 14 díxitos decimais correctos por termo.^[30]

Irracionalidade e transcendencia

Non todos os avances matemáticos relacionados con π tiñan como obxectivo aumentar a precisión das aproximacións. Cando Euler resolveu o problema de Basilea en 1735, achando o valor exacto da suma dos cadrados recíprocos, estableceu unha conexión entre π e os números primos que máis tarde contribuíu ao desenvolvemento e estudo da función zeta de Riemann:^[33]

$\frac{π^{2}}{6} = \frac{1}{1^{2}} + \frac{1}{2^{2}} + \frac{1}{3^{2}} + \frac{1}{4^{2}} + \dots$ O científico suízo Johann Heinrich Lambert demostrou en 1768 que π é un número irracional, o que significa que non é igual ao cociente de dous números enteiros calquera.Modelo:Sfn A proba de Lambert explotou unha representación de fracción continua da función tanxente.^[34] O matemático francés Adrien-Marie Legendre demostrou en 1794 que π² tamén é irracional. En 1882, o matemático alemán Ferdinand von Lindemann demostrou que π é un número transcendental,^[35] confirmando unha conxectura feita tanto por Legendre como por Euler.Modelo:Sfn^[36] Hardy e Wright afirman que "as probas foron posteriormente modificadas e simplificadas por Hilbert, Hurwitz e outros escritores".^[37]

Adopción do símbolo π

Modelo:Multiple image Nos primeiros usos, a letra grega π utilizábase para denotar o semiperímetro (semiperipheria en latín) dun círculo^[38] e combinábase en proporcións con δ (para diámetro ou semidiámetro) ou ρ (para raio) para formar constantes de círculo.^[39]^[40]^[41]^[42] (Antes diso, os matemáticos ás veces utilizaban letras como c ou p no seu lugar.Modelo:Sfn) O primeiro uso rexistrado é o de Oughtred Modelo:Nobr, para expresar a relación entre periferia e diámetro nas edicións de 1647 e posteriores de Modelo:Lang.^[43]Modelo:Sfn Barrow igualmente utilizada Modelo:Nobr para representar a constante Modelo:Math,^[44] mentres que Gregory utilizaba no seu lugar Modelo:Nobr para representar Modelo:Math.^[45]^[41]

O uso máis antigo coñecido da letra grega π para representar a relación entre a circunferencia dun círculo e o seu diámetro foi realizado polo matemático galés William Jones na súa obra de 1706 Modelo:Lang; ou, A new Introduction to the Mathematics.^[22]Modelo:Sfn A letra grega aparece na p. 243 na frase " $\frac{1}{2}$ Periferia π)", calculada para un círculo de raio un. Con todo, Jones escribe que as súas ecuacións para π proveñen da "pluma lista do verdadeiramente enxeñoso Sr. John Machin", o que leva a especular que Machin puido empregar a letra grega antes que Jones.Modelo:Sfn A notación de Jones non foi adoptada inmediatamente por outros matemáticos, e a notación de fraccións seguía utilizándose en 1767.^[39]^[46]

Euler empezou a utilizar a forma dunha soa letra a partir do seu Ensaio explicativo das propiedades do aire de 1727, aínda que utilizou Modelo:Math, o cociente entre a periferia e o raio, neste e nalgúns escritos posteriores.^[47]^[48] Euler utilizou por primeira vez Modelo:Nowrap na súa obra de 1736 Mechanica,^[49] e continuou na súa moi lida obra de 1748 Introductio in analysin infinitorum (escribiu: «co fin da menor brevidade escribiremos este número como Modelo:Pi; así Modelo:Pi é igual á metade da circunferencia dun círculo de raio Modelo:Math").^[50] Como Euler mantiña unha gran correspondencia con outros matemáticos de Europa, o uso da letra grega estendeuse rapidamente, e a práctica adoptouse universalmente a partir de entón no mundo occidental,Modelo:Sfn aínda que a definición seguía variando entre Modelo:Math e Modelo:Math até 1761.^[51]

Busca moderna de máis díxitos

Era da informática e algoritmos iterativos

Modelo:Cadro de citas

O desenvolvemento dos computadores a mediados do século XX revolucionou de novo a procura de díxitos de Modelo:Pi. Os matemáticos John Wrench e Levi Smith alcanzaron os 1.120 díxitos en 1949 utilizando unha calculadora de escritorio.Modelo:Sfn Utilizando unha serie infinita de tanxente inversa (arctan), un equipo dirixido por George Reitwiesner e John von Neumann conseguiu ese mesmo ano 2.037 díxitos cun cálculo que requiriu 70 horas de computador no ENIAC.Modelo:Sfn^[52] A marca, sempre baseado nunha serie arctan, bateuse repetidamente (3089 díxitos en 1955,^[53] 7.480 díxitos en 1957; 10.000 díxitos en 1958; 100.000 díxitos en 1961) hasta alcanzar el millón de díxitos en 1973.Modelo:Sfn

Dous desenvolvementos adicionais ao redor de 1980 aceleraron de novo a capacidade de calcular Modelo:Pi. En primeiro lugar, o descubrimento de novos algoritmos iterativos para calcular Modelo:Pi, que eran moito máis rápidos que as series infinitas; e en segundo lugar, a invención de algoritmos de multiplicación rápida que podían multiplicar grandes números moi rapidamente.Modelo:Sfn Estes algoritmos son especialmente importantes nos cálculos Modelo:Pi modernos porque a maior parte do tempo do computador dedícase á multiplicación.Modelo:Sfn Entre eles inclúense o algoritmo de Karatsuba, a multiplicación de Toom-Cook e os métodos baseados na transformada de Fourier.Modelo:Sfn

Os algoritmos iterativos foron publicados de forma independente en 1975-1976 polo físico Eugene Salamin e o científico Richard Brent.Modelo:Sfn Estes evitan depender de series infinitas. Un algoritmo iterativo repite un cálculo específico, utilizando en cada iteración os resultados dos pasos anteriores como entradas, e produce un resultado en cada paso que converxe ao valor desexado. O enfoque foi inventado en realidade máis de 160 anos antes por Carl Friedrich Gauss, no que agora se denomina o método da media aritmético-xeométrica (método AGM) ou algoritmo de Gauss-Legendre.Modelo:Sfn Modificado por Salamin e Brent, tamén se coñece como algoritmo de Brent-Salamin.

Os algoritmos iterativos utilizáronse amplamente despois de 1980 porque son máis rápidos que os algoritmos de series infinitas: mentres que as series infinitas adoitan aumentar o número de díxitos correctos de forma aditiva en termos sucesivos, os algoritmos iterativos xeralmente «multiplican» o número de díxitos correctos en cada paso. Por exemplo, o algoritmo de Brent-Salamin duplica o número de díxitos en cada iteración. En 1984, os irmáns John e Peter Borwein crearon un algoritmo iterativo que cuadriplica o número de díxitos en cada paso; e en 1987, un que aumenta o número de díxitos cinco veces en cada paso.^[54] O matemático xaponés Yasumasa Kanada utilizou métodos iterativos para establecer varias marcas no cálculo de Modelo:Pi entre 1995 e 2002.^[55] Esta rápida converxencia ten un prezo: os algoritmos iterativos requiren moita máis memoria que as series infinitas.^[55]

Motivacións para a computación de Modelo:Pi

Para a maioría dos cálculos numéricos que implican Modelo:Pi, un puñado de díxitos proporciona suficiente precisión. Segundo Jörg Arndt e Christoph Haenel, trinta e nove díxitos son suficientes para realizar a maioría dos cálculos cosmolóxicos, porque esa é a precisión necesaria para calcular a circunferencia do universo observable cunha precisión dun átomo. Tendo en conta os díxitos adicionais necesarios para compensar os erros de redondeo computacionais, Arndt conclúe que uns poucos centos de díxitos serían suficientes para calquera aplicación científica. A pesar disto, a xente traballou arduamente para calcular Modelo:Pi até miles e millóns de díxitos.^[56] Este esforzo pode atribuírse en parte á compulsión humana por bater marcas, e tales logros con Modelo:Pi adoitan ser noticia en todo o mundo.^[57]^[58] Tamén teñen beneficios prácticos, como probar supercomputadoras, probar algoritmos de análise numérica (incluídos algoritmos de multiplicación de alta precisión) e, dentro das matemáticas puras, proporcionar datos para avaliar a aleatoriedade dos díxitos de Modelo:Pi.Modelo:Sfn

Serie rapidamente converxente

As calculadoras modernas de Modelo:Pi non utilizan exclusivamente algoritmos iterativos. Nas décadas de 1980 e 1990 descubríronse novas series infinitas que son tan rápidas como os algoritmos iterativos, pero máis simples e con menor consumo de memoria.^[55] Os algoritmos iterativos rápidos anticipáronse en 1914, cando o matemático indio Srinivasa Ramanujan publicou ducias de novas fórmulas innovadoras para Modelo:Pi, notables pola súa elegancia, profundidade matemática e rápida converxencia.^[59] Unha das súas fórmulas, baseada en ecuacións modulares, é $\frac{1}{π} = \frac{2 \sqrt{2}}{9801} \sum_{k = 0}^{\infty} \frac{(4 k)! (1103 + 26390 k)}{k!^{4} (39 6^{4 k})} .$

Notas

Modelo:Listaref

Véxase tamén

Modelo:Commonscat

Número pi

Índice

Definicións

A probabilidade e o número π