Función monótona

Figura 1. Gráfica dunha función monótona (función crecente).

Figura 2. Gráfico dunha función monótona (función decrecente).

Figura 3. Gráfica dunha función que non é monótona.

En matemáticas, unha función monótona é unha función entre conxuntos ordenados que conserva ou inverte a orde. No primeiro caso, fálase dunha función crecente e no outro de función decrecente. Este concepto apareceu por primeira vez na análise real de funcións numéricas e despois xeneralizouse no marco máis abstracto da teoría da orde.

Monotonía na análise real

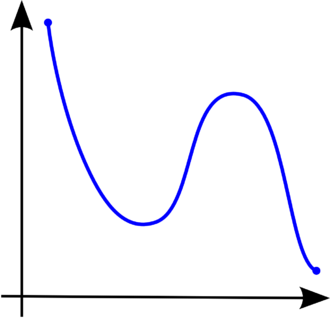
Intuitivamente (ver as figuras ao lado), a representación gráfica dunha función monótona nun intervalo é unha curva que “sobe» constantemente ou «baixa» constantemente. Se este aspecto gráfico é inmediatamente revelador, non é, porén, a única forma na que se revela a propiedade da monotonía: unha función monótona é unha función que sempre ten o mesmo efecto sobre a relación de orde. Para unha función crecente, a orde que existe entre dúas variábeis atópase na orde das súas imaxes, para unha función decrecente, a orde das imaxes invírtese en comparación coa orde dos antecedentes.

Para unha función con derivada nun intervalo, o estudo da monotonía está ligado ao estudo do signo da derivada, que é constante: sempre positivo ou sempre negativo.

Definición

Sexa $I$ un intervalo de $ℝ$ e $f$ unha función de valores reais, cuxo dominio de definición contén este intervalo $I$.

Monotonía en sentido amplo. Dise que $f$ é  :

• crecente (ou: crecente en sentido amplo) sobre $I$ se

para todo par $(x,y)\in I^2$ tal que $x<y$, temos $f(x)⩽f(y)$;

• decrecente (ou : decrecente en sentido amplo) sobre $I$ se

para todo par $(x,y)\in I^2$ tal que $x<y$, temos $f(x)⩾f(y)$;

• monótona (ou: monótona no sentido amplo) en $I$ se é crecente en $I$ ou decrecente en $I$.

Exemplo: para todo real $x$, denotado $E(x)$ a parte enteira de $x$ (é o único enteiro relativo $k$ tal que $k⩽x<k+1$). A función $E:ℝ\to ℝ$ vai crecendo en $ℝ$ pero non é estritamente crecente (ver máis abaixo), porque é constante en cada intervalo $[i,i+1[$ de extremos enteiros.

Estritamente monótona. Dise que $f$ é:

• estritamente crecente en $I$ se

para todo par $(x,y)\in I^2$ tal que $x<y$, temos $f(x)<f(y)$;

• estritamente decrecente en $I$ se

para todo par $(x,y)\in I^2$ tal que $x<y$, temos $f(x)>f(y)$;

• estritamente monótona sobre $I$ se é estritamente crecente en $I$ ou estritamente decrecente en $I$.

Exemplos : sexa $n$ un enteiro estritamente positivo.

• A función $f:{ℝ}_{+}\to ℝ:x\mapsto x^n$, é estritamente crecente en ${ℝ}_{+}$ .
  En efecto, se $a,b,a^{\prime }$ e $b^{\prime }$ son números reais tal que $0⩽a<b$ e $0⩽a^{\prime }<b^{\prime }$, entón $a{a}^{\prime }<b{b}^{\prime }$. Deducimos por indución sobre o número enteiro $n$ que para calquera parella $(x,y)$ de positivos reais ou ceros tal que $x<y$, temos $x^n<y^n$.
• Cando $n$ é impar, a función $f:ℝ\to ℝ:x\mapsto x^n$, é estritamente crecente en $ℝ$.
• De feito, é estritamente crecente en ${ℝ}_{+}$ (ver o exemplo anterior) e impar.

Nota 1: para que unha función $f$ sexa crecente (respectivamente estritamente crecente) en $I$, é necesario e suficiente que $-f$ sexa decrecente (resp. estritamente decrecente) en $I$.

Nota 2 : para que unha función monótona $f:I\to ℝ$ non o sexa estritamente, é necesario (e desde logo é suficiente) que $I$ conteña un intervalo non trivial (é dicir, non baleiro e non reducido a un punto) no que $f$ é constante.

Propiedades elementais

Operacións alxébricas

Sexan dúas funcións crecentes $I$. Temos:

• a súa suma é crecente;
• se teñen valores positivos, o seu produto é crecente.

Existe a propiedade análoga para funcións estritamente crecentes.

Composición

Sexan dúas funcións $f:I\to ℝ$ e $g:J\to ℝ$, onde $I$ e $J$ son dous intervalos reais tal que $f(I)\subset J$; podemos definir a función composta $g\circ f:I\to ℝ$.

Se $f$ é monótona en $I$ e $g$ é monótona en $J$, daquela $g\circ f$ é monótona en $I$. Máis precisamente :

• se $f$ e $g$ ambos as dúas son crecentes ou decrecentes, entón $g\circ f$ é crecente;
• se unha das dúas funcións $f$ ou $g$ é crecente e a outra decrecente, entón $g\circ f$ é decrecente.

Exste a propiedade análoga para as funcións estritamente monótonas.

Inxectividade

Unha función estritamente monótona nun intervalo $I$ é inxectiva, é dicir que dous elementos de $I$ distintos teñen imaxes distintas.

Esta propiedade, combinada co teorema do valor intermedio, é útil para atopar o número de ceros nunha función.

Propiedades relativas á continuidade e límites

Teorema do límite monótono para unha función

Sexa $]a,b[$ un intervalo aberto (limitado ou non) e unha función crecente $f:]a,b[\to ℝ$ . Así:

• $f$ admite en todos os puntos $x$ de $]a,b[$ un límite pola esquerda e un límite pola dereita, finitos, que denotamos respectivamente $f(x^{-})$ e $f(x^{+})$; verifican a dobre desigualdade $f(x^{-})⩽f(x)⩽f(x^{+})$;
• $f$ admite un límite pola esquerda $b$, finito ou igual a $+\mathrm{\infty }$; este límite é finito se e só se $f$ é maior.
• $f$ admite un límite pola dereita en $a$, finito ou igual a $-\mathrm{\infty }$; este límite é finito se e só se $f$ é menor.

Un teorema análogo para funcións decrecentes dedúcese inmediatamente substituíndo $f$ por $-f$.

Un corolario deste teorema é a continuidade de calquera sobrexección monótona dun intervalo sobre un intervalo.

Puntos de descontinuidade

Teorema de Froda (1929): o conxunto $D$ de puntos de descontinuidade dunha función monótona é finito ou numerábel (dicimos que é numerábel como máximo ). Efectivamente, denotando ${\epsilon }_x=f(x^{+})-f(x^{-})$, a familia ${\left({\epsilon }_x\right)}_{x\in D\cap [c,d]}$ de reais estritamente positivos é sumábel e, polo tanto, como moito numerábel para todos os $[c,d]$ incluídos no intervalo de monotonía. Froda demostrou de feito que para calquera función real, o conxunto de puntos de descontinuidade do primeiro tipo é como moito numerábel. Ou para unha función monótona, o teorema do límite monótono di exactamente que este tipo de descontinuidade é a única posíbel.

Monotonía e signo da derivada

Un uso clásico e importante do cálculo diferencial é a caracterización, entre as funcións diferenciábeis (dunha variábel real, e con valores reais), das que son monótonas (en sentido amplo ou en sentido estrito) nun intervalo.

Teorema: Modelo:Teorema

Observacións

• Dedúcese que unha condición suficiente para que unha función derivábel $f:I\to ℝ$ sexa estritamente crecente en $I$ é que para todo $x\in I,f^{\prime }(x)>0$. Pero esta condición non é de ningún xeito necesaria, como mostra o enunciado do teorema e os dous exemplos seguintes.
• Este teorema xeneralízase a funcións continuas nun intervalo mais derivábeis só no complemento dun subconxunto numerábel: cf. Teorema do valor medio.

Exemplo 1

A función $f:ℝ\to ℝ:x\mapsto x^3$, é estritamente crecente en $ℝ$. O criterio anterior permítenos volver demostralo:

• é derivábel, e para todo real $x,f^{\prime }(x)=3x^2$;
• a maiores, o conxunto de puntos onde desaparece a súa derivada é $\{0\}$; é de interior baleiro.

Exemplo 2

A función $f:ℝ\to ℝ:x\mapsto \cos x+x$, é estritamente crecente en $ℝ$. De feito:

• é derivábel, e para calquera real $x,f^{\prime }(x)=1-\sin x⩾0$;
• a maiores, o conxunto de puntos onde desaparece a súa derivada é $\left(\frac{\pi }{2}\right)+2\pi \mathbb{Z}=\{x\in ℝ\mid \mathrm{\exists }k\in \mathbb{Z},x=\left(\frac{\pi }{2}\right)+2k\pi \}$, que é internamente baleiro (mesmo é contábel).

Exemplo 3

A función $f:[-1,1]\to ℝ:x\mapsto \arccos x+\arcsin x$ é constante. En efecto, as derivadas de $\arccos$ e $\arcsin$, definidas en $]-1,1[$, son opostas entre si e en $]-1,1[,f^{\prime }$ é cero e $f$ é constante. Así, para todo $x$ En $]-1,1[$ (e mesmo en $[-1,1]$, por continuidade), $f(x)=f(0)=\frac{\pi }{2}$ .

Monotonía na topoloxía

Unha aplicación $f:X\to Y$ entre dous espazos topolóxicos dise que é monótona se cada unha das súas fibras é conexa, é dicir que para todos os $y$ en $Y$ o conxunto $f^{-1}(y)$ (que pode estar baleiro) é conexo.

Monotonía na análise funcional

En análise funcional, un operador $T:X\to X^{*}$ nun espazo vectorial topolóxico $X$ (que pode ser non linear) chámase operador monótono se

$(Tu-Tv,u-v)\ge 0\mathrm{\forall }u,v\in X.$

O teorema de Kachurovskii  mostra que as derivadas das funcións convexas nos espazos de Banach son operadores monótonos.

A monotonía na teoría da orde

A teoría da orde trata de conxuntos parcialmente ordenados e conxuntos preordenados en xeral, ademais dos intervalos reais. A definición anterior de monotonía tamén é relevante nestes casos. Por exemplo, considere unha aplicación $f$ dun conxunto ordenado $(A,{⩽}_A)$ nun conxunto ordenado $(B,{⩽}_B)$.

• $f$ chámase aplicación crecente (respectivamente, aplicación estritamente crecente) se conserva a orde (respectivamente, a orde estritamente), é dicir, se dous elementos $x$ e $y$ de $A$ verifican $x{⩽}_{A}y$ (resp. $x{<}_{A}y$ ), e as súas respectivas imaxes por $f$ verifican $f(x){⩽}_{B}f(y)$ (respectivamente, $f(x){<}_{B}f(y)$ ).
• $f$ chámase aplicación decrecente (resp. aplicación estritamente decrecente ) se inverte a orde (resp. a orde estritamente), é dicir, se dous elementos $x$ e $y$ de $A$ verifican $x{⩽}_{A}y$ (resp. $x{<}_{A}y$ ), e as súas respectivas imaxes por $f$ verifican $f(x){⩾}_{B}f(y)$ (resp. $f(x){>}_{B}f(y)$ )

As aplicacións monótonas son fundamentais na teoría da orde. Algunhas aplicacións monótonas notábeis son os mergullos de ordes (aplicacións para as que $x⩽y$ se e só se $f(x)⩽f(y)$ e os isomorfismos de orde (os mergullos de orde que son sobrexectivos).

Véxase tamén

Outros artigos

• Operador monótono.

Modelo:Control de autoridades