Vector

Modelo:1000 artigos icona título Modelo:Outroshomónimos

Un vector en física e mais no cálculo vectorial é un concepto caracterizado por un valor, é dicir, un escalar (magnitude numérica), e por un sentido (que pode ser definido nun espazo 3-dimensional, ou en xeral p-dimensional). Os vectores utilízanse para describir magnitudes vectoriais tales como velocidades, aceleracións ou forzas, nas cales é importante considerar non só o valor senón tamén a dirección e máis o sentido.

Aínda que frecuentemente se describa a un vector por un número de "compoñentes", cada un deles dependente do sistema de coordenadas particular que se use, as propiedades dun vector non dependen do sistema de coordenadas usado para o describir.

Un exemplo común dun vector é a forza. Ten un valor e unha orientación en tres dimensións (a diferenza de moitas dimensións espaciais, que teñen dúas), e a suma múltipla das forzas de acordo coa lei do paralelogramo.

En matemáticas, un vector é un elemento dunha estrutura alxébrica chamada espazo vectorial, que esencialmente é un conxunto de elementos cun conxunto de axiomas que debe satisfacer cada un deles.

Matematicamente un vector pode ser tamén un conxunto de elementos ordenados entre si mais, a diferenza dun conxunto normal como o dos números naturais, neste caso o conxunto está ordenado.

Represéntase por un segmento orientado para denotar o seu sentido (o da frecha), a súa magnitude (a lonxitude da frecha) e mais o punto de onde parte. Para este tipo de vectores (xeralmente bi ou tridimensionais) defínense módulo, dirección e sentido.

Notación

Compoñentes dun vector nun sistema tridimensional.

Os eixos do sistema de coordenadas descríbense xeralmente empregando as letras x, y e z, xeramente o eixo z representa o perpendicular ao plano. Os vectores pódense representar con letras, cunha frecha enriba ( $\vec{a}$ ), ou simplemente en letra grosa ( $𝐚$ ). As coordenadas ou compoñentes dun vector nun sistema de referencia poden escribirse entre parénteses e separadas con comas: Modelo:Ecuación

No espazo vectorial de tres dimensións empréganse tres compoñentes:

Modelo:Ecuación

Outro xeito típico de anotar un vector nas tres dimensións é definilo como a combinación dos vectores unitarios cartesianos i, j e k:

Modelo:Ecuación

Modelo:Áncora Compoñentes dun vector

Modelo:Ver tamén Como se comentou anteriormente, un vector descríbese a miúdo por un conxunto de compoñentes vectoriais que suman para formar o vector dado. Normalmente, estes compoñentes son as proxeccións do vector nun conxunto de eixos de referencia mutuamente perpendiculares (vectores base). Dise que o vector pode descompoñerse en relación a eses vectores base.

A descomposición^[1] dun vector en compoñentes non é único, porque depende da escolla dos eixos sobre os que se proxecta o vector.

Alén diso, non é obrigatorio o uso de vectores unitarios cartesianos como $\hat{𝐱}, \hat{𝐲}, \hat{𝐳}$ como base no que representar un vector. Os vectores tamén se poden expresar en termos de outra base arbitraria, incluíndo os vectores unitarios dun sistema de coordenadas cilíndrico ( $\hat{ρ}, \hat{ϕ}, \hat{𝐳}$ ) ou un sistema de coordenadas esféricas ( $\hat{𝐫}, \hat{θ}, \hat{ϕ}$ ). As dúas últimas opcións son máis convenientes para resolver problemas que posúen simetría cilíndrica ou esférica, respectivamente.

A escolla dunha base non afecta ás propiedades dun vector nin ao seu comportamento baixo transformacións.

Un vector tamén se pode dividir en relación a vectores de base "non fixos" que mudan a súa orientación en función do tempo ou do espazo. Por exemplo, un vector no espazo tridimensional pódese descompoñer en relación a dous eixos, respectivamente normal e tanxente a unha superficie (ver figura).

Outra descomposición pode ser nunha compoñente radial e outra compoñente tanxencial que están relacionadas co raio de rotación dun obxecto. A primeira é paralela ao raio e a segunda é ortogonal a el.^[2]

Nestes casos, cada un dos compoñentes pode descompoñerse á súa vez en relación a un sistema de coordenadas fixo ou conxunto de bases (por exemplo, un sistema de coordenadas global ou sistema de referencia inercial).

Exemplo 1

Nun plano, usualmente, temos a base cos vectores unitarios do eixo Modelo:Mvar, $\vec{x} = (1, 0)$ , e do eixo Modelo:Mvar, $\vec{y} = (0, 1)$ .

O vector $\vec{v} = (4, 3)$ pódese descompoñer como $\vec{v} = 4 \vec{x} + 3 \vec{y}$ .

Exemplo 2

Sexa $P_{3}$ o espazo de todos os polinomios alxébricos de grao como máixmo 3 (isto é, o expoñente máis alto de x só pode ser 3). este espazo é linear e xerado polos seguintes polinomios:

B_{P} = {1, x, x^{2}, x^{3}}

que forman a seguinte base

1 : = [\begin{matrix} 1 \\ 0 \\ 0 \\ 0 \end{matrix}]; x : = [\begin{matrix} 0 \\ 1 \\ 0 \\ 0 \end{matrix}]; x^{2} : = [\begin{matrix} 0 \\ 0 \\ 1 \\ 0 \end{matrix}]; x^{3} : = [\begin{matrix} 0 \\ 0 \\ 0 \\ 1 \end{matrix}]

así o vector de coordenadas correspondente ao polinomio sería

p (x) = a_{0} + a_{1} x + a_{2} x^{2} + a_{3} x^{3}

como vector columna

[\begin{matrix} a_{0} \\ a_{1} \\ a_{2} \\ a_{3} \end{matrix}] .

Segundo esa representación, o operador de diferenciación d/dx que denotamos como D estará representado pola seguinte matriz:

D p (x) = P^{'} (x); [D] = [\begin{matrix} 0 & 1 & 0 & 0 \\ 0 & 0 & 2 & 0 \\ 0 & 0 & 0 & 3 \\ 0 & 0 & 0 & 0 \end{matrix}]

Usando ese método é fácil explorar as propiedades do operador, como: invertibilidade, hermitiano ou anti-hermitiano ou ningún dos dous, espectro e eigenvalores, etc.

Propiedades

Un vector ten as seguintes propiedades:

- Punto de aplicación, é a orixe do vector.

- Módulo, expresa o valor numérico da magnitude vectorial. Represéntase pola lonxitude do segmento, sempre en valor absoluto. Por exemplo, se se quere expresar que o módulo de $\vec{a}$ vale 5 unidades, faise así: $| \vec{a} | = 5 u$ . Expresado con fórmulas, dado un vector $\vec{a}$ de coordenadas $(a_{x}, a_{y}, a_{z})$ o seu módulo é $| \vec{a} | = \sqrt{a_{x}^{2} + a_{y}^{2} + a_{z}^{2}}$ .

- Dirección, que é a da recta soporte, que se expresa matematicamente cunha ecuación de recta, que se lle chama liña de acción.

- Sentido, distinguíndose dous sentidos sobre a recta de aplicación do vector, graficamente, a punta da frechiña.

Clasificación dos vectores

Segundo o seu punto de aplicación:

- Vector fixo, que ten un punto de aplicación definitorio, do que non se despraza.

- Vectores deslizantes, o seu punto de aplicación pode estar en calquera punto dunha recta soporte definida.

- Vector libre, non ten relevancia o seu punto de aplicación.

Outros vectores significantes:

- Vector unitario, un vector cuxo módulo é unha unidade, que se calcula: $\vec{u_{a}} = \frac{(a_{x}, a_{y}, a_{z})}{| \vec{a} |}$ . Os vectores unitarios correspondentes a (1,0,0), (0,1,0) e (0,0,1) denomínanse $\hat{ı}$ , $\hat{ȷ}$ e $\hat{k}$ , sendo $\hat{ı}$ o vector unitario do eixe do x, $\hat{ȷ}$ o vector unitario do eixo y, e $\hat{k}$ o do z.

- Vector oposto a outro é o que ten o mesmo punto de aplicación, módulo e dirección mais sentido contrario. Así o vector oposto a $\vec{a}$ é $- \vec{a}$ .

- Vectores equipolentes, vectores con igual módulo e sentido, e rectas soporte paralelas e, entón, tamén distintos puntos de aplicación.

- Vectores paralelos, que teñen coordenadas proporcionais entre si (equipolentes con distinto módulo, por exemplo).

- Vectores concorrentes, cando teñen o mesmo punto de aplicación, no caso de vectores fixos, ou cando simplemente teñen un punto en común (punto de concorrencia).

- Vectores coplanares, todos os vectores están contidos no mesmo plano.

- Vectores colineares, que comparten unha mesma recta de acción

Suma e resta de vectores

Método gráfico

A suma e resta de vectores ten en conta, ademais da magnitude escalar ou módulo, o sentido das magnitudes intervenientes. Nas figuras achegadas nesta páxina esquematízase o método gráfico para buscar o resultado.

Método do paralelogramo

Consiste en pór graficamente os dous vectores de xeito que as respectivas orixes coincidan nun punto, completando o resto do paralelogramo por paralelas. O resultado da suma é a diagonal de dito paralelogramo.

Método do triángulo

Consiste en poñer graficamente un vector a continuación doutro, facendo coincidir o extremo inicial dun vector co extremo final do outro vector. O vector suma resultante forma un triángulo canda estes dous vectores, que corresponde ao lado oposto ao vértice dos vectores colocados correctamente, ou dito doutro xeito, vai dende a orixe dun vector até a fin do outro (a e b respectivamente no debuxo adxacente)

Método analítico

A suma

Con dous vectores de coordenadas,

\vec{a} = (a_{x}, a_{y}, a_{z})

\vec{b} = (b_{x}, b_{y}, b_{z})

o resultado da suma é:

\vec{a} + \vec{b} = [(a_{x} + b_{x}), (a_{y} + b_{y}), (a_{z} + b_{z})]

A resta

Para restar dous vectores libres $\vec{a}$ e $\vec{b}$ súmase $\vec{a}$ co oposto de $\vec{b}$ :

\vec{a} - \vec{b} = \vec{a} + (- \vec{b})

O resultado da resta é:

\vec{a} - \vec{b} = [(a_{x} - b_{x}), (a_{y} - b_{y}), (a_{z} - b_{z})]

Módulo resultante

Dados dous vectores $\vec{a}$ e $\vec{b}$ , de módulos coñecidos e que forman o ángulo $θ$ entre si, pódese obter o módulo $| \vec{a} + \vec{b} |$ coa seguinte fórmula:

$| \vec{a} + \vec{b} | = \sqrt{{| \vec{a} |}^{2} + {| \vec{b} |}^{2} + 2 | \vec{a} | | \vec{b} | \cos θ}$

Dedución da expresión

Sexan dous vectores $\vec{a}$ e $\vec{b}$ que forman un ángulo $θ$ entre si:

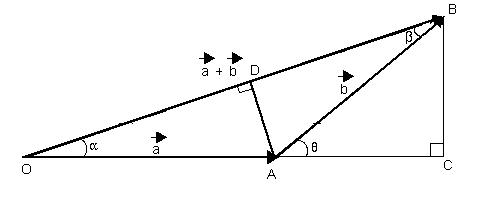
A fórmula para calcular $| \vec{a} + \vec{b} |$ dedúcese observando os triángulos rectángulos que se forman, OCB e ACB, e aplicando o Teorema de Pitágoras. No triángulo OCB:

$O B^{2} = O C^{2} + C B^{2}$

$O B = | \vec{a} + \vec{b} |$

$O C = | \vec{a} | + A C$

Resultando:

${| \vec{a} + \vec{b} |}^{2} = {(| \vec{a} | + A C)}^{2} + C B^{2}$

No triángulo ACB :

$\frac{A C}{| \vec{b} |} = \cos θ$

$A C = | \vec{b} | \cos θ$

$\frac{C B}{| \vec{b} |} = s e n θ$

$C B = | \vec{b} | s e n θ$

Substituíndo isto na igualdade de antes resulta:

${| \vec{a} + \vec{b} |}^{2} = {(| \vec{a} | + | \vec{b} | \cos θ)}^{2} + ({| \vec{b} | s e n θ)}^{2}$

${| \vec{a} + \vec{b} |}^{2} = | \vec{a} |^{2} + 2 | \vec{a} | | \vec{b} | \cos θ + {| \vec{b} |}^{2} \cos^{2} θ + {| \vec{b} |}^{2} s e n^{2} θ$

${| \vec{a} + \vec{b} |}^{2} = | \vec{a} |^{2} + 2 | \vec{a} | | \vec{b} | \cos θ + {| \vec{b} |}^{2} (\cos^{2} θ + s e n^{2} θ)$

$\cos^{2} θ + s e n^{2} θ = 1 \to {| \vec{a} + \vec{b} |}^{2} = | \vec{a} |^{2} + 2 | \vec{a} | | \vec{b} | \cos θ + {| \vec{b} |}^{2}$

$| \vec{a} + \vec{b} | = \sqrt{| \vec{a} |^{2} + 2 | \vec{a} | | \vec{b} | \cos θ + {| \vec{b} |}^{2}}$

$| \vec{a} + \vec{b} | = \sqrt{| \vec{a} |^{2} + {| \vec{b} |}^{2} + 2 | \vec{a} | | \vec{b} | \cos θ}$

Obtención da Dirección

Para obter os ángulos $α, β$ directores no anterior exemplo temos que coñecer o ángulo $θ$ e ter calculado $| \vec{a} + \vec{b} |$ .

Podemos usar esta fórmula:

$\frac{| \vec{b} |}{s e n α} = \frac{| \vec{a} |}{s e n β} = \frac{| \vec{a} + \vec{b} |}{s e n θ}$

Coa fórmula obteremos os seos, despois para achar o ángulo a partir do seo temos que ter en conta que:

$α + β = θ$

Produto dun vector por un escalar

O produto dun vector cun escalar é outro vector que conserva a dirección orixinal, o seu módulo é o produto do escalar polo módulo do vector e o sentido é o mesmo ou oposto segundo o escalar sexa positivo ou negativo respectivamente.

Graficamente sería poñer, sobre a mesma recta da dirección, o módulo tantas veces como marque o escalar, e de ser negativo, viralo sentido do vector (mire o debuxo).

Analiticamente, un número $n$ e un vector $\vec{a}$ , o produto $n \vec{a}$ realízase multiplicando cada unha das compoñentes do vector polo escalar. Dado o vector de tres compoñente

\vec{a} = (a_{x}, a_{y}, a_{z})

o seu produto polo escalar é

n 𝐚 = (n a_{x}, n a_{y}, n a_{z})

é dicir, multiplícase por $n$ cada unha das compoñentes do vector.

Ángulo entre dous vectores

Dados os vectores $\vec{a} = (a_{x}, a_{y}, a_{z})$ e $\vec{b} = (b_{x}, b_{y}, b_{z})$ , o ángulo $θ$ calcúlase polo seu coseno:

c o s θ = \frac{a_{x} b_{x} + a_{y} b_{y} + a_{z} b_{z}}{| \vec{a} | | \vec{b} |}

Isto deriva do produto escalar.

Produto escalar

Modelo:Artigo principal

Modelo:Ecuación

Produto vectorial

Modelo:Artigo principal

Modelo:Ecuación

Véxase tamén

Outros artigos

Ligazóns externas

Modelo:Control de autoridades

↑ Gibbs, J.W. (1901). Vector Analysis: A Text-book for the Use of Students of Mathematics and Physics, Founded upon the Lectures of J. Willard Gibbs, by E.B. Wilson, Chares Scribner's Sons, New York, p. 15
↑ Modelo:Cite web

[1] Gibbs, J.W. (1901). Vector Analysis: A Text-book for the Use of Students of Mathematics and Physics, Founded upon the Lectures of J. Willard Gibbs, by E.B. Wilson, Chares Scribner's Sons, New York, p. 15

[2] Modelo:Cite web

[1]

[2]

Vector

Índice