Cristalografía de raios X

Un difractómetro de raios X de po en movemento.

Proceso de determinación da estrutura dunha molécula por cristalografía de raios X.

A cristalografía de raios X é unha técnica experimental para o estudo e análise de materiais, baseada no fenómeno da difracción dos raios X por sólidos en estado cristalino.

Os raios X son difractados polos electróns que rodean os átomos por ser a súa lonxitude de onda da mesma orde de magnitude que o raio atómico. O feixe de raios X que emerxe tras esta interacción contén información sobre a posición e tipo de átomos encontrados no seu camiño. Os cristais, grazas á súa estrutura periódica, dispersan elasticamente os feixes de raios X en certas direccións e amplifícanos por interferencia construtiva, orixinando un padrón de difracción. Existen varios tipos de detectores especiais para observar e medir a intensidade e posición dos raios X difractados, e a súa análise posterior por medios matemáticos permite obter unha representación a escala atómica dos átomos e moléculas do material estudado.

Max von Laue realizou os primeiros experimentos de cristalografía de raios X en 1912. Von Laue, William Henry Bragg e William Lawrence Bragg desenvolveron inicialmente a teoría de difracción de cristais, tarefa á que axiña se sumaron outros científicos. Ao longo do século XX tiveron lugar varios avances teóricos e técnicos, como a aparición das supercomputadoras e o uso de sincrotróns para a produción de raios X, que incrementaron a capacidade do método para determinar as propiedades estruturais de todo tipo de moléculas: sales, materiais inorgánicos complexos, proteínas e mesmo compoñentes celulares como os ribosomas. É posible traballar con monocristais ou con po microcristalino, conseguíndose diferentes datos en ambos os casos: para as aplicacións que requiren só unha caracterización precisa dos parámetros da rede cristalina, pode ser suficiente unha difracción de raios X por po, pero para unha determinación precisa das posicións atómicas é preferible traballar con monocristais.

Dada a relación existente entre a estrutura tridimensional das moléculas e as súas propiedades químicas e físicas, a cristalografía contribuíu ao avance en varias disciplinas científicas como a química, a bioloxía molecular, a xeoloxía, a física aplicada e a ciencia de materiais. A ampla dispoñibilidade de tubos de raios X, complementada co desenvolvemento de fontes de raios X de alta intensidade aumentou significativamente o seu impacto nestes campos de investigación e tamén en áreas con aplicacións industriais, como o desenvolvemento de fármacos e a mineraloxía aplicada. A maior limitación deste método é a necesidade de traballar con sistemas cristalinos, polo que non é aplicable a disolucións, a sistemas biolóxicos in vivo, a sistemas amorfos ou a gases. Nalgúns casos, os raios X poden romper os enlaces químicos que manteñen a integridade estrutural, o que ten como resultado un modelo distorsionado da molécula estudada. Este problema afecta especialmente os materiais de interese biolóxico.

Historia

Primeiros experimentos

Modelo:Imaxe múltiple A idea de que os cristais son unha repetición periódica dun grupo de moléculas xa existía antes de que Wilhelm Conrad Röntgen descubrise os raios X en 1895. Aínda que as distancias típicas entre os planos da rede cristalina se descoñecían, sabíase que debían ser moi pequenas comparadas coa lonxitude de onda da luz visible. Isto deulle ao físico alemán Max von Laue a idea de utilizar cristais de sulfato de cobre para determinar se os raios X se compoñían de partículas ou ondas: deduciu que, se fosen ondas, deberían xerar un padrón de difracción ao atravesar os cristais. Os experimentos realizáronse en 1912 coa axuda de Walter Friedrich e Paul Knipping, ambos os dous antigos estudantes de Röntgen. Estes experimentos confirmaron a presenza de difracción cristalina, interpretada por von Laue como a extensión a tres dimensións da difracción de Fraunhofer por unha grella.

Pouco despois, os británicos William Henry Bragg e William Lawrence Bragg (pai e fillo respectivamente) reproduciron o experimento. W.L. Bragg explicou a difracción como a interferencia dos raios X reflectidos por planos cristalinos paralelos, introducindo a descrición coñecida desde entón como lei de Bragg. En 1913, Paul Ewald demostrou que as dúas interpretacións dos resultados publicadas independentemente por von Laue e Bragg eran equivalentes. Von Laue recibiu o premio Nobel de Física en 1914 polo seu descubrimento do fenómeno, e os Bragg recibiron o mesmo premio un ano máis tarde polo seu traballo nas aplicacións prácticas. Cara ao final da década, lográrase determinar as lonxitudes de onda dos raios X e a estrutura de varios compostos inorgánicos simples e establecéranse as bases teóricas da técnica grazas ao traballo dos xa mencionados investigadores e de Charles Galton Darwin e Peter Debye, entre outros.

O desenvolvemento da técnica: 1920-1960

O período entre 1920 e 1960 caracterizouse por importantes adiantos metodolóxicos que propiciaron o emprego da difracción de raios X para analizar estruturas de moléculas máis complexas.

Durante a década de 1920 os avances da teoría cuántica serviron para caracterizar con máis precisión a interacción entre os raios X e os átomos dos cristais; isto posibilitou a análise correcta da intensidade da difracción. Na mesma época apareceron as táboas para determinar a simetría cristalina a partir da distribución de reflexións no padrón de difracción e empezaron a usarse as series de Fourier para representar a distribución de electróns na rede cristalina. Os desenvolvementos na representación matemática da densidade electrónica continuaron ata a segunda guerra mundial, facilitando a obtención das primeiras estruturas de moléculas orgánicas. En 1935, o cristalógrafo británico Arthur Patterson descubriu un truco matemático para obter as distancias interatómicas directamente a partir dos datos experimentais, o que supuxo un importante avance na análise da difracción.

Entre as décadas de 1940 e 1960, xurdiron outros procedementos para a determinación de estruturas, especialmente, métodos heurísticos baseados no proceso de ensaio e erro, que demostraron ser bastante exactos en combinación con restricións condicionantes baseadas nas propiedades físicas dunha estrutura correcta, como por exemplo, que a densidade electrónica debe ser sempre positiva. Neste período a cristalografía empezou a adquirir importancia no campo da química orgánica, proceso que culminou coa determinación en 1957 da estrutura da vitamina B12, un proxecto liderado por Dorothy Hodgkin.

Avances en cristalografía de macromoléculas: 1960-1980

O adianto máis trascendente durante as décadas de 1960 e 1970 foi o recoñecemento da cristalografía de proteínas e de moléculas implicadas en procesos biolóxicos en xeral como área de investigación clave na bioloxía molecular. O ano 1962 foi especialmente relevante ao outorgárense dous premios Nobel polos resultados obtidos usando métodos cristalográficos nesa área: o premio Nobel de Química concedeuse a Max Perutz e John Kendrew polos seus estudos cristalográficos das proteínas hemoglobina e mioglobina e o premio Nobel de Medicina a Francis Crick, James Watson e Maurice Wilkins por descubrir que o ADN forma unha dobre hélice. En 1964 Dorothy Hodgkin tamén obtivo o premio Nobel de Química pola determinación de varias estruturas de importancia biolóxica, como a penicilina e a vitamina B12, entre outras.

Un adianto que facilitou en gran medida o éxito das técnicas cristalográficas tanto no caso de macromoléculas orgánicas cun gran número de átomos coma no de moléculas de menor tamaño foi o desenvolvemento de ordenadores dixitais; grazas a eles foi posible usar programas para medir e analizar doadamente os datos obtidos nos experimentos en vez de realizar os laboriosos cálculos manualmente. Porén, ao final deste período o estudo de proteínas estaba aínda limitado pola ausencia de fontes de rayos X intensos e o emprego de película fotográfica para medir os padróns de difracción, o que requiría un longo proceso de revelado e dixitalización das imaxes. A consecuencia destas limitacións, e malia o reconñecemento xeneralizado do potencial da cristalografía para estes experimentos, a finais da década de 1970 o Banco de Datos de Proteínas só contaba cunhas sesenta entradas.

Expansión e madureza: 1980-2010

Os tubos de raios X, con sucesivas melloras, utilizáronse como a fonte primordial de raios X para os experimentos de cristalografía desde os seus comezos ata a década de 1970, época en que se empezou a experimentar coa radiación de sincrotrón de raios X. Os sincrotróns dedicados exclusivamente á produción de raios X apareceron na década de 1980 e o seu número non deixou de aumentar desde entón. Na primeira década do século XXI construíronse os primeiros láseres de electróns libres de raios X, con capacidade de producir feixes de luz pulsada dunha intensidade varias ordes de magnitude maior que nas fontes de luz sincrotrón convencionais. A duración dos pulsos de luz, da orde de femtosegundos ofrece a posibilidade de observar cambios nos cristais a escalas temporais inacadables anteriormente. Durante estes anos tamén se desenvolveron novos detectores bidimensionais ou «de área», capaces de xerar directamente unha imaxe dixitalizada do padrón de difracción. Estes detectores facilitaron a rápida medición e análise da difracción e substituíron totalmente as placas fotográficas usadas ata entón.

Os mencionados avances, unidos ao incremento da capacidade dos computadores modernos para almacenar e procesar datos, permitiron levar a cabo experimentos antano irrealizables, e desembocaron nun aumento exponencial do número de estruturas dilucidadas por métodos cristalográficos. O desenvolvemento máis notable tivo lugar na área das macromoléculas orgánicas, con máis de 88 000 estruturas depositadas no Banco de Datos de Proteínas ao comezo de 2013. A obtención en 2000 da estrutura do ribosoma, un enorme complexo formado por ácidos nucleicos e varias proteínas onde ten lugar a síntese de proteínas na célula, ilustra as capacidades que acadou a técnica.

Aspectos físicos

Cristais e redes cristalinas

Estrutura cristalina do cloruro de hidróxeno deuterado coa cela unidade superposta sobre as moléculas. A rede cristalina fómase por medio da translación da cela unidade ao longo das direccións definidas por $a,b$ e $c$.

Parámetros da cela unidade.

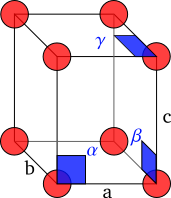
Os cristais están formados por unha repetición periódica de moléculas en tres dimensións. O cristal pódese representar matematicamente como unha rede tridimensional, chamada «rede de Bravais», na que todas as intersecciónss, ou nodos, son idénticas.Modelo:Harvnp O paralelepípedo definido polas liñas entre distintos nodos da rede coñécese como cela unidade; aínda que para unha rede dada sexa posible designar múltiples celas unidade que cumpran esta definición, por convención escóllese habitualmente a de menor volume que reflicte a simetría do cristal.Modelo:Harvnp A cela unidade defínese pola lonxitude dos seus lados $a$, $b$ e $c$ na dirección dos tres eixes espaciais e os ángulos $\alpha$, $\beta$ e $\gamma$ que os eixes da rede forman entre si. As coordenadas de calquera punto da rede cristalina pódense expresar como unha combinación lineal dos vectores $𝐚$, $𝐛$ e $𝐜$.

A posición dun átomo na cela unidade exprésase como coordenadas fraccionarias de $𝐚$, $𝐛$ e $𝐜$ da seguinte forma:

$R=x𝐚+y𝐛+z𝐜$

coas coordenadas ($x$, $y$, $z$) comprendidas entre 0 e 1.Modelo:Harvnp

O obxectivo dos experimentos de difracción de raios X é descubrir o valor de $x$, $y$ e $z$ para cada átomo. Para conseguilo cómpre, en primeiro lugar, determinar a relación entre a rede cristalina e a xeometría do padrón de difracción e, en segundo lugar, obter as posicións dos átomos a partir da intensidade da difracción.

Raios X

Representación esquemática dunha onda electromagnética, mostrando a oscilación periódica dos campos eléctrico e magnético.

Os raios X son un tipo de radiación electromagnética con lonxitudes de onda entre 10 e Modelo:Nowrap ou enerxías entre 0,1 e Modelo:Nowrap.Modelo:Harvnp Para os experimentos de difracción cristalina adoitan usarse raios X de enerxía relativamente alta, da orde de Modelo:Nowrap, correspondente a lonxitudes de onda da orde de Modelo:Nowrap.Modelo:HarvnpModelo:Harvnp

Os raios X descríbense matematicamente como unha onda sinusoidal que se propaga a través do espazo. Tomando un punto arbitrario como orixe, o valor do campo eléctrico $E$ en función do tempo $t$ pódese escribir como:Modelo:Harvnp

$E(t)=A\exp (2\pi ict/\lambda )$

$A$ é a amplitude da oscilación, $\lambda$ a lonxitude de onda e $c$ a velocidade da luz. A consecuencia da interacción cos electróns dos átomos na mostra, a onda sofre un desfase $\alpha$ con respecto á onda no punto de orixe:

$E(t)=A\exp (2\pi ict/\lambda )\exp (2\pi i\alpha )$

A diferenza de fase depende da distancia entre o punto de orixe e os átomos do material; isto implica que a estrutura atómica, é dicir, as posicións que ocupan os átomos, pódese derivar da fase dos raios X que atravesaron o material.

Dispersión elástica de raios X

O fenómeno da difracción cristalina ten a súa orixe na dispersión elástica ou scattering elástico do feixe de raios X polos átomos do cristal. Neste tipo de interacción, o electrón desvía os raios X, que toman exactamente a mesma traxectoria que un raio de luz visible reflectido nun espello, é dicir, os raios dispersados emerxen nun ángulo $2\theta$ con respecto á dirección dos raios incidentes. Tanto o electrón coma os raios X conservan a súa enerxía inicial durante esta interacción.Modelo:Harvnp

A dispersión elástica por un grupo de átomos nunha dirección dada póidese cuantificar cunha cantidade coñecida como factor de estrutura que é igual á suma dos raios reflectidos por cada átomo $j$ que interacciona cos raios incidentesModelo:Harvnp

$𝐅(𝐒)=\sum _j{f}_j\exp (2\pi i{𝐫}_j\cdot 𝐒)$

$f$ é unha función chamada factor de forma atómica (ou factor de dispersión atómica) que describe a dispersión por todos os electróns do átomo en conxunto. A dispersión elástica atómica depende do número atómico $Z$ e do ángulo de incidencia dos raios X. O cambio de fase dos raios dispersados durante a interacción vén dada polo produto escalar de ${𝐫}_j$, o vector entre a orixe e cada átomo $j$ e $𝐒$, coñecido como vector de dispersión, con magnitude $2\sin \theta /\lambda$ e dirección perpendicular ao plano virtual de reflexión.

Difracción cristalina

Lei de Bragg

A difracción nunha dirección dada débese esencialmente á relación entre as fases de todas as ondas reflectidas por cada cela unidade do cristal nesa dirección. Os raios que atravesaron distintos puntos do cristal seguen camiños ópticos de diferente lonxitude e esta diferenza dá lugar a un cambio na amplitude da onda resultante; cando a diferenza de fase é de 180 graos, as ondas anúlanse entre si. Ao contrario, cando as ondas están en fase, a amplitude da onda final é a suma das amplitudes para cada onda. Como un cristal está composto dun gran número de celas unidade, a interferencia construtiva entre todas elas ten como resultado un feixe intenso dabondo como para poder medirse cun detector de raios X.

Lei de Bragg: Os átomos ou grupos de átomos na rede cristalina están representados por esferas (para simplificar o diagrama, a terceira dimensión do cristal non se representa). As esferas sitúanse sobre planos imaxinarios paralelos, perpendiculares ao diagrama, separados por $d$. Os raios X inciden sobre os planos cun ángulo $\theta$. Na imaxe da esquerda, a diferenza no camiño percorrido polas ondas dispersadas polos dous planos é un múltiplo enteiro da lonxitude de onda; por tanto, as ondas emerxentes están en fase e obsérvase difracción cun ángulo $\theta$ respecto aos planos de difracción ou $2\theta$ respecto ao feixe incidente. Á dereita, cun ángulo de incidencia diferente, a lei de Bragg non se cumpre para esta familia de planos cristalinos; as ondas emerxentes están desfasadas e non se observa difracción.

A condición para que as ondas estean en fase é que a diferenza dos seus camiños ópticos sexa cero ou un múltiplo enteiro $n$ da lonxitude de onda. Nun cristal, a diferenza no camiño óptico entre átomos situados en posicións equivalentes en distintas celas unidade é $2d\sin \theta$ onde $d$ é a distancia entre os planos imaxinarios que unen os puntos equivalentes da rede cristalina. Isto significa que para que se observe interferencia construtiva de raios X a un ángulo de observación $2\theta$, débese cumprir a expresión coñecida como lei de Bragg:

$n\lambda =2d\sin \theta$

Como no caso da dispersión elástica por un átomo, a difracción cristalina pódese interpretar como a reflexión especular dos raios X por todos os planos do cristal cun ángulo $\theta$ do feixe incidente e separados entre si pola distancia $d$ que cumpre a lei de Bragg. Por este motivo, os puntos do padrón de difracción denomínanse «reflexións».

Índices de Miller: A figura mostra exemplos de diferentes planos de difracción nunha cela unidade, ilustrando a correspondencia entre os índices de Miller $hkl$ e a orientación dos planos no sistema de coordinadas definido por aquela.

Índices de Miller

Para que se cumpra a lei de Bragg para un grupo de planos de reflexión paralelos, estes deben cruzar os eixes da cela unidade un número enteiro de veces. As reflexións cristalinas identifícanse por medio de tres números $h$, $k$ e $l$ iguais ao número de interseccións dos planos cos eixes $a$, $b$ e $c$ da cela. Os números $h$, $k$ e $l$ reciben o nome de índices de Miller. Matematicamente, os índices de Miller describen un vector perpendicular ao plano de reflexión no sistema de coordenadas definido pola rede cristalina.

A rede recíproca

Denomínse rede recíproca a transformada de Fourier da rede cristalina. Esta construción matemática facilita a representación dos planos de reflexión e a visualización da relación entre a orientación do cristal e o padrón de difracción. As coordenadas de cada punto da rede recíproca coinciden cos índices de Miller, é dicir, cada punto da rede recíproca representa unha familia de planos de Miller no espazo real da rede cristalina; a distancia da orixe a cada punto da rede é $1/d$.Modelo:Harvnp

Igual que no caso da rede cristalina, os puntos da rede recíproca pódense expresar como unha combinación lineal de vectores ${𝐚}^{\ast }$, ${𝐛}^{\ast }$ e ${𝐜}^{\ast }$:

$𝐎𝐇=h{𝐚}^{\ast }+k{𝐛}^{\ast }+l{𝐜}^{\ast }$

A relación entre os parámetros da cela unidade ($a$, $b$, $c$, $\alpha$, $\beta$, $\gamma$) de volume $V$ e a cela unidade recíproca ($a^{\ast }$, $b^{\ast }$, $c^{\ast }$, ${\alpha }^{\ast }$,${\beta }^{\ast }$, ${\gamma }^{\ast }$) é a seguinte:Modelo:Harvnp

$a^{\ast }=\frac{bc\sin \alpha }{V};b^{\ast }=\frac{ac\sin \beta }{V};c^{\ast }=\frac{ab\sin \gamma }{V}$

$V^{\ast }=a^{\ast }{b}^{\ast }{c}^{\ast }\sqrt{1-{\cos }^2{\alpha }^{\ast }-{\cos }^2{\beta }^{\ast }-{\cos }^2{\gamma }^{\ast }+2\cos {\alpha }^{\ast }\cos {\beta }^{\ast }\cos {\gamma }^{\ast }}$

$\cos {\alpha }^{\ast }=\frac{\cos \beta \cos \gamma -\cos \alpha }{\sin \beta \sin \gamma };\cos {\beta }^{\ast }=\frac{\cos \alpha \cos \gamma -\cos \beta }{\sin \alpha \sin \gamma };\cos {\gamma }^{\ast }=\frac{\cos \alpha \cos \beta -\cos \gamma }{\sin \alpha \sin \beta }$

Representación bidimensional da construción de Ewald. Os raios X incidentes están representados polo vector de onda ${𝐊}_i$, de amplitude $1/\lambda$. A rede recíproca represéntase en azul; para simplificar o diagrama só se mostran as coordenadas dalgúns puntos da rede, representando os planos de Miller correspondentes. O punto (4,1) coincide coa superficie da esfera; por tanto, observarase un feixe de raios X co vector de onda ${𝐊}_f$ reflectido na dirección dada por $2\theta$. A magnitude do vector diferenza entre ${𝐊}_i$ e ${𝐊}_f$ ou vector de difracción é a distancia entre os planos paralelos de índices (4,1).

A esfera de Ewald

Para visualizarmos doadamente os planos de Miller que contribúen á difracción nunha dirección dada e determinar a relación entre a orientación do cristal e o padrón de difracción, utilízase a construción coñecida como esfera de Ewald. A esfera de Ewald ilustra todas as posibles direccións nas que os raios X poden ser reflectidos polo cristal. O raio desta esfera é $1/\lambda$ e o seu extremo na dirección do feixe de raios X incidente coincide coa orixe da rede recíproca.

Se un punto da rede recíproca de coordenadas $(h,k,l)$ se encontra sobre a superficie da esfera de Ewald, os planos de Miller con índices $(h,k,l)$ darán lugar a un punto de difracción na dirección definida polo centro da esfera e ese punto da rede recíproca. A distancia entre a orixe e $(h,k,l)$ é $1/d$, polo que se pode demostrar xeometricamente que esta condición de difracción é equivalente á lei de Bragg.

O factor de estrutura cristalino

O vector con coordenadas $(h,k,l)$ na rede recíproca é perpendicular ao plano de reflexión e a súa magnitude é $1/d=2\sin \theta /\lambda$; é dicir, é un vector de dispersión $𝐒$, introducido na definición do factor de estrutura $𝐅(𝐒)$, para o que se cumpre a lei de Bragg. Por tanto, o factor de estrutura na dirección definida polos planos de Miller descritos polos índices $(h,k,l)$ reformúlase como

${𝐅}_{hkl}=\sum _j{f}_j\exp (2\pi i{𝐫}_j\cdot 𝐒)=\sum _j{f}_j\exp (2\pi i(x_{j}h+y_{j}k+z_{j}l))$

onde $(x,y,z)$ é o vector de coordenadas do átomo $j$ no sistema definido pola cela unidade e a suma realízase para todos os átomos contidos nela. En lugar de sumar as contribucións de cada átomo, tamén se pode realizar unha integración sobre os electróns no volume $V$ da cela unidade, cuxa distribución por elemento de volume se representa pola función de densidade electrónica Modelo:NowrapModelo:Harvnp

${𝐅}_{hkl}=\underset{x}{\int }\underset{y}{\int }\underset{z}{\int }\rho (x,y,z)\exp (2\pi i(xh+yk+zl))dxdydz$

Representación vectorial da lei de Friedel en ausencia de absorción. As magnitudes dos factores de estrutura relacionados por esta lei, coñecidos como «pares Friedel», son iguais e as súas fases, opostas.

A aplicación das operacións de simetría do cristal ás coordenadas $(x,y,z)$ ten como resultado relacións de igualdade entre os factores de estrutura de diferentes reflexións. Ás reflexións así relacionadas denomínaselles «simetricamente equivalentes». Nos experimentos cristalográficos, onde o grupo de simetría non se coñece con certeza a priori, compáranse as reflexións relacionadas por diversas operacións de simetría para caracterizar a simetría do cristal. A igualdade entre os módulos ou «amplitudes» das reflexións relacionadas por un centro de inversión, con índices de Miller $(h,k,l)$ e $(-h,-k,-l)$

$|{𝐅}_{hkl}|=|{𝐅}_{\overline{h}\overline{k}\overline{l}}|$

coñécese como lei de Friedel e ocorre mesmo en ausencia de simetría, á parte da translación da cela unidade sobre a rede cristalina.Modelo:Harvnp Na práctica a lei de Friedel non se cumpre exactamente debido á presenza de interaccións inelásticas entre os raios X e os átomos, que teñen como resultado a absorción de enerxía por estes. Eses efectos adoitan ser pequenos comparados coas interaccións elásticas e non se adoitan ter en conta, agás para lonxitudes de onda na veciñanza dunha descontinuidade de absorción do cristal.

O problema das fases

O propósito dos experimentos cristalográficos non é obter o padrón de difracción, senón o valor da función de distribución electrónica $\rho (x,y,z)$, o que permite determinar a posición dos átomos e a estrutura tridimiensional da molécula cristalina. Pódese demostrar que $\rho (x,y,z)$ pode representarse como sumas de Fourier dos factores de estrutura en todas as direccións:Modelo:Harvnp

$\rho (x,y,z)=\frac{1}{V}\sum _h\sum _k\sum _l|{𝐅}_{hkl}|\exp (-2\pi i(xh+yk+zl))$

Mentres que o módulo do factor de estrutura é simplemente a raíz cadrada da intensidade do punto de difracción, medida por un detector sensible aos raios X, a fase non se pode computar directamente. Isto coñécese como o «problema das fases». Existen varios métodos para resolver o problema des fases e dilucidar a estrutura atómica, clasificados nos seguintes grupos:

• Métodos de Patterson
• Métodos directos
• Dispersión anómala
• Reemprazamento isomorfo
• Reemprazamento molecular

Método de Patterson

A función de Patterson calcúlase efectuando a síntese de Fourier co cadrado dos factores de estrctura $|{𝐅}_{hkl}{|}^2$ como coeficientes. Esta función pódese calcular directamente a partir dos datos experimentais, ao non depender da fase dos factores de estrutura. En 1935, Arthur Patterson decatouse de que os máximos desta función corresponden aos vectores que se poden trazar entre cada par de átomos na cela unidade, o cal se pode utilizar en certos casos favorables para determinar a posición de todos ou algúns átomos. En particular, a análise da función de Patterson utilízase a miúdo para localizar os átomos causantes de diferenzas isomorfas ou anómalas, o cal é á súa vez o primeiro paso para solucionar o problema das fases por estes outros métodos.Modelo:HarvnpModelo:Harvnp

Métodos directos

A función de distribución de densidade electrónica $\rho (x,y,z)$ caracterízase por ser sempre positiva e acadar valores máximos arredor dos átomos. Estas e outras propiedades derivadas de principios básicos, expresadas en forma matemática, utilízanse para discriminar entre valores das fases que dan como resultado unha estrutura con características fisicamente posibles e os que non o dan e, por eliminación destes últimos, dilucidar a estrutura da molécula de interese. Este método úsase correntemente para resolver o problema das fases para moléculas pequenas.Modelo:Harvnp En contraste, no caso dos cristais de macromoléculas, os métodos directos non adoitan ser dabondo para resolver a estrutura totalmente ab initio sen ningunha información experimental adicional; isto débese a que, por un lado, os cristais de proteínas e moléculas de similar tamaño raramente difractan a unha resolución suficiente para obter o número de reflexións requirido para determinar todos os parámetros atómicos e, por outro lado, ao gran número de átomos na cela unidade, que causa que as relacións entre as probabilidades das fases sexan menos determinantes que nos casos de moléculas que contan con poucos átomos.

Malia os límites do método, os seus principios tamén se aplican na área de difracción de macromoléculas para mellorar as fases obtidas por outros métodos e o cálculo das fases a partir dun modelo de baixa resolución. Na cristalografía de proteínas, as propiedades claves para discriminar entre fases correctas e incorrectas inclúen:

• O contraste entre as zonas da cela unidade ocupadas por moléculas de auga ou solvente en estado amorfo e as zonas ordenadas ocupadas pola molécula.
• Unha distribución característica da probabilidade de valores da densidade electrónica.

Igual que a función de Patterson, os métodos directos tamén se utilizan para determinar as posicións de átomos especiais nos métodos de substitución ou reemprazamento isomorfo e de dispersión anómala.

Reemprazamento isomorfo

O reemprazamento isomorfo ou substitución isomorfa é un método para resolver o problema das fases empregado predominantemente en cristalografía de macromoléculas. Consiste na introdución no medio de cristalización dun composto químico de pequeno tamaño que contén un átomo pesado, é dicir, dun número atómico elevado. Os compostos de mercurio, platino, uranio e ouro son os máis utilizados, entre moitos outros. Para que o método teña éxito debe establecerse un enlace químico entre a molécula de interese e o átomo pesado, e a molécula modificada ou «derivada» debe formar cristais isomorfos, coa mesma simetría que os obtidos a partir da molécula «nativa» sen modificar. O factor de estrutura da molécula derivada ${𝐅}_{hkl}^{PH}$ é a suma do factor de estrutura «nativo» ${𝐅}_{hkl}^P$ e a contribución do átomo pesado ${𝐅}_{hkl}^H$.

As fases do átomo pesado que contribúen a isto pódense calcular por métodos directos a partir das diferenzas ${𝐅}^{PH}-{𝐅}^P$. Aínda que unha soa substitución isomorfa non é suficiente para determinar ${𝐅}^P$, se se repite o proceso con polo menos unha segunda estrutura derivada diferente, é posible determinar as fases para a estrutura nativa, polo método coñecido como reemprazamento isomorfo múltiple ou as súas siglas en inglés MIR (Multiple Isomorphous Replacement)

A principal limitación deste método é a dificultade de encontrar compostos que reaccionen coa molécula a estudar sen destruír ao mesmo tempo o cristal ou modificar sensiblemente a súa simetría ou as dimensións da cela unidade.

Dispersión anómala

Valores das compoñentes do factor de estrutura anómalo f" e f' arredor dun salto de absorción.

O factor de forma atómica $f$ non só describe a dispersión elástica senón tamén o efecto fotoeléctrico, que ten lugar cando os electróns cambian o seu estado cuántico ao absorber parte da enerxía dos raios X. O termo que corresponde á dispersión inelástica ou «anómala» é un número complexo $f_A=f{\text{'}}_A+i{f}^{\prime }{\text{'}}_A$. Ambas as compoñentes, real $f{\text{'}}_A$ e imaxinaria $f^{\prime }{\text{'}}_A$, alteran a magnitude dos factores de estrutura. A compoñente imaxinaria, relacionada co coeficiente de absorción, introduce ademais un cambio de fase que dá como resultado diferentes magnitudes dos pares Friedel ${𝐅}_{hkl}$ e ${𝐅}_{\overline{h}\overline{k}\overline{l}}$, idénticas en ausencia deste efecto.

A contribución anómala ao factor de estrutura é menor que a contribución elástica $f_0$ e a miúdo non é necesario tela en conta. Porén, $f_A$ depende da lonxitude de onda dos raios X e experimenta grandes variacións cando a enerxía do feixe incidente é similar á enerxía dun nivel atómico do átomo. Cando $f{\text{'}}_A$ e $f^{\prime }{\text{'}}_A$ acadan os seus valores máximos os cambios na magnitude e fase dos factores de estrutura poden ser significativos. Se algúns átomos na molécula son afectados por este tipo de interacción, pódense achar as súas posicións na cela unidade analizando as diferenzas de intensidade entre as mesmas reflexións medidas a distintas lonxitudes de onda, ou entre os pares de Friedel á mesma lonxitude de onda. Ditas diferenzas pódense utilizar para resolver o problema das fases polo método MAD (Multiwavelength Anomalous Dispersion/Diffraction ou ‘dispersión/difracción anómala a múltiples lonxitudes de onda’) ou SAD (Single-wavelength Anomalous Dispersion/Diffraction ou ‘dispersión/difracción anómala a unha soa lonxitude de onda’)

A maioría dos átomos pesados usados no método de reemprazamento isomorfo exhiben unha dispersión anómala importante no rango de lonxitudes de onda usado nos experimentos cristalográficos, polo cal estas dúas técnicas se usan ás veces conxuntamente. A vantaxe dos métodos baseados na dispersión anómala é que, ao precisaren en principio só un cristal para determinar as fases, non están limitados por un isomorfismo imperfecto. O uso de radiación sincrotrón, que se pode sintonizar ás lonxitudes de onda que optimizan a dispersión anómala, deu lugar a un forte incremento da popularidade do método entre os científicos.

Reemprazamento molecular

O método de reemprazamento molecular consiste no emprego dunha molécula de estrutura coñecida para calcular as fases iniciais dunha segunda molécula con elementos estruturais comúns coa primeira. Este é o método máis usado para determinar a estrutura de macromoléculas como as proteínas, xa que moitas delas se agrupan en familias cunha estrutura similar ou forman complexos supramoleculares nos que se coñece a estrutura dunha ou máis compoñentes.

A desvantaxe do reemprazamento molecular é que as fases obtidas están nesgadas cara á estrutura utilizada como punto de partida, o que non ocorre coas técnicas baseadas enteiramente nos datos de difracción experimentais e coñecemento a priori das propiedades químicas ou estruturais do material. O éxito deste método depende de algoritmos sofisticados para detectar e eliminar este nesgo durante o refinamento das fases.

A obtención das fases permite calcular un mapa de densidade electrónica (mostrado en branco), a partir do cal se constrúe o modelo da estrutura. O modelo adoita consistir en liñas, representando os enlaces atómicos, ou puntos, representando átomos individuais. Na figura úsanse ambas as representacións.

Refinamento da estrutura

Unha vez calculada a función $\rho (x,y,z)$ a partir das fases, pódese construír un modelo da estrutura no mapa de densidade electrónica, descrito por varios parámetros: as posicións de cada átomo $x_j$, $y_j$ e $z_j$, o seu factor de temperatura $B_j$ representando os deprazamentos dos átomos con respecto á súa posición media etc.Modelo:Harvnp A determinación inicial destes parámetros pode ser incorrecta, debido a erros na determinación das fases ou fallos de interpretación da densidade electrónica. Durante o refinamento, modifícase reiteradamente o modelo e seguidamente compárase o módulo dos factores de estrutura ${𝐅}_c$ calculados a partir deste co dos factores de estrutura experimentais $𝐅$, ata que a diferenza entre ambos sexa mínima. Utilízase para a comparación o factor R, definido como:Modelo:Harvnp

$R=\frac{\sum ||𝐅|-|{𝐅}_c||}{\sum |𝐅|}$

A suma realízase sobre todas as reflexións $hkl$.

Úsanse dúas técnicas matemáticas para axustar os parámetros do modelo durante o refinamento: os mínimos cadrados e a máxima verosimilitude. O segundo método require máis recursos computacionais, pero é máis xeral e aplícase con preferencia en problemas difíciles, como macromoléculas e difracción a baixa resolución.Modelo:Harvnp

Cristalización

Esquema ilustrativo do método de difusión de vapor para obter cristais para o seu estudo por raios X.

Unha adecuada cristlización é moi importante nesta técnica. Para obtermos datos de difracción dun cristal, este debe cumprir certos requisitos en canto a tamaño, pureza e regularidade da rede cristalina. Aínda que por veces é posible utilizar cristais de metais ou minerais inorgánicos formados por medios naturais, a miúdo cómpre preparalos por recristalización ou precipitación do material nunha solución líquida sobresaturada en condicións controladas de concentración e temperatura. No método de cristalización por difusión de vapor, a solución que contén o material a cristalizar xunto cun precipitante acada un estado de equilibrio termodinámico con outra solución máis concentrada do precipitante, por difusión do disolvente cara a esta a través do aire; esta técnica úsase tanto para moléculas de poucos átomos coma para proteínas e outras macromoléculas. Un segundo método é a cristalización en xeles, moi útil para cristalizar materiais insolubles; esta técnica, lenta comparada coa difusión de vapor, consiste na introdución dun reactivo nun xel antes de que este endureza. Posteriormente, introdúcese outra solución dun segundo reactivo na capa superior do xel, desde onde difunde ao resto da matriz e reacciona coa primeira substancia para dar lugar a cristais.

As condicións de preparación de cristais deben tamén ser as axeitadas para que se obteñan cristais dun tamaño óptimo para o seu estudo por difracción de raios X; o tamaño ideal está determinado pola densidade e composición da mostra: mentres que os cristais de gran tamaño amortecen excesivamente os raios X e adoitan presentar irregularidades na matriz cristalina, os de tamaño moi pequeno difractan feblemente. No caso de cristais de materiais orgánicos, son preferibles os cristais dunhas décimas de milímetro; porén, cando se usan fontes de raios X moi intensas, como láseres de electróns libres ou líñas de luz sincrotrón modernas, é posible traballar con cristais de dimensiónsa duns vinte μm ou mesmo menores. Para as aplicacións de cristalografía en po, cómpren polo menos varios centos de miligramos de material machacado ata formar cristais de aproximadamente dez μm ou menores.

Adquisición de datos

Fontes de raios X

Estación de sincrotrón para experimentos de cristalografía que usa o método de rotación. O feixe de raios X, dun par de décimas de mm diríxese ao cristal, de aproximadamente o mesmo tamaño, desde a esquerda da imaxe. O cristal sitúase sobre un difractómetro, que permite orientar e xirar o cristal para obter un conxunto de reflexións o más completo posible. O padrón de difracción grávase no detector bidimensional mostrado á dereita, neste caso unha pantalla de material sensible aos raios X conectada a unha cámara de CCD por medio de fibra óptica.

Os experimentos de cristalografía de raios X pódense realizar cun tubo de raios X ou usando a radiación sincrotrón emitida por aceleradores de partículas. Nos tubos de raios X, aplícase unha voltaxe para acelerar un feixe de electróns producidos por quentamento dun filamento de volframio (o cátodo). Os electróns acelerados coliden contra un material metálico (o ánodo) e durante a conseguinte desaceleración emiten radiación de Bremsstrahlung de espectro continuo, é dicir, composta de múltiples lonxitudes de onda. O ánodo absorbe parte dos raios X emitidos polos electróns e emite á súa vez raios X das lonxitudes de onda características do metal. Por exemplo, un ánodo de cobre emite principalmente na lonxitude de onda de 1,5405 Å. A radiación de Bremsstrahlung e outras liñas de emisión características menos intensas fíltranse cun metal absorbente. No exemplo do ánodo de cobre, utilízase níquel, que é bastante transparente aos raios X de Modelo:Nowrap pero absorbe eficazmente a radiación a lonxitudes de onda menores, obténdose un feixe de raios X bastante monocromático.Modelo:Harvnp Os tubos de raios X son relativamente baratos e os laboratorios de investigación adoitan utilizalos para realizar experimentos in situ.

A radiación sincrotrón obtense cando un feixe de electróns acelerados ata alcanzaren unha velocidade próxima á da luz é desviado da súa traxectoria por medio dun campo magnético. A radiación sincrotrón é de espectro continuo e a lonxitude de onda desexada para o experimento pode seleccionarse cun monocromador. As fontes de radiación sincrotrón emiten raios X moito máis intensos que os xerados polos tubos e son necesarias para mellorar a calidade da difracción cando os cristais son moi pequenos ou están compostos de átomos lixeiros, que interaccionan debilmente cos raios X.

Detectores

Existen varios tipos de detectores que se usan nos experimentos de cristalografía. O detector bidimensional que foi máis usado durante moito tempo foi a película fotográfica, actualmente substituída por outros detectores máis sensibles aos raios X. Outro detector clásico é o contador proporcional unidimensional, normalmente un detector de escintilacións, instalado nun difractómetro e controlado por computador. Este tipo de detector mide as reflexións unha a unha e aínda se usa para a cristalografía de moléculas pequenas, pero é pouco eficaz nos experimentos con macromoléculas, onde o número de reflexións é de entre 10 000 e 100 000.Modelo:Harvnp

A partir da década de 1990 empezaron a aparecer novos detectores, como as «placas de imaxe» (image plates). As placas de imaxe están cubertas dun material fosforescente, onde os electrones incrementan a súa enerxía ao absorberen os raios X difractados e son atrapados neste nivel en centros de cor. Os electróns liberan a enerxía ao iluminarse a placa con luz láser, emitindo luz con intensidade proporcional á da reflexión. Estes detectores son unha orde de magnitude máis sensibles que a película fotográfica e posúen unha marxe dinámica superior en varias ordes de magnitude, o que facilita a medición simultánea das reflexións máis intensas e as máis febles. Outros detectores usados na actualidade son detectores electrónicos, coñecidos como detectores «de área», que procesan o sinal inmediatamente trala detección dos raios X. Poden ser cámaras de ionización ou unha placa fosforescente acoplada a unha cámara CCD.Modelo:Harvnp Nos anos 2000 empezáronse a utilizar fotodiodos aliñados formando unha placa, denominados PAD (Pixel Array Detectors). Estes detectores caracterízanse por unha gran marxe dinámica e un tempo morto entre imaxes moi baixo, da orde de milisegundos.

Xeometrías de difracción

Existen tres métodos para medir a difracción de raios X: o método de Laue, o método de rotación e o de po.

Método de Laue

Padrón de difracción obtido polo método de Laue en transmisión: as reflexións dispostas ao longo dunha curva son xeradas por unha mesma lonxitude de onda.

Consiste en facer incidir nun cristal un espectro continuo de raios X, de tal maneira que para cada lonxitude de onda se cumpre a lei de Bragg para diferentes puntos da rede recíproca. Isto fai posible medir todas ou case todas as reflexións sen cambiar a orientación do cristal. Existen dúas variantes do método de Laue: transmisión e reflexión. No método de Laue por transmisión, o cristal colócase entre a fonte de raios X e o detector. No método de reflexión o detector encóntrase entre a fonte e o cristal, para detectar os feixes difractados cara a atrás.

Malia ser o método utilizado nos primeiros experimentos cristalográficos, o método de Laue usábase moi pouco para a determinación de estruturas debido principalmente á baixa intensidade da radiación de espectro continua producida polos tubos de raios X en comparación coa emisión característica monocromática. O crecente uso da radiación sincrotrón fomentou o rexurdimento do método. A capacidade de medir todos os datos necesarios para a determinación da estrutura nun curto tempo convérteo no método máis axeitado para o estudo de reaccións químicas que teñen lugar en poucos segundos, como catálises por encimas e ceolitas e os efectos de perturbacións causadas por campos eléctricos, cambios de presión e temperatura etc. en diversos materiais.Modelo:Harvnp

Métodos de rotación de cristal

Padrón de difracción obtido por rotación dun cristal. O uso de computadores para a interpretación das imaxes obtidas por este método transformouno no modo preferido de medición de datos na maioría das aplicacións.

Padrón de difracción obtido polo método de precesión. Este método dá lugar a unha representación sen distorsións dos planos da rede recíproca.

Faise incidir un feixe de raios X monocromáticos sobre un cristal, que rota a unha velocidade constante arredor dun eixe perpendicular aos raios X. A rotación do cristal causa que todos os puntos da rede recíproca atravesen consecutivamente a esfera de Ewald, conseguindo así medir as reflexións necesarias. Existen diferentes variantes deste método. No método de Weissenberg úsase unha cámara de forma cilíndrica que rodea o cristal de tal maneira que o eixe de rotación do cristal coincide co eixe do cilindro. A cámara trasládase a medida que o cristal xira para que as reflexións estean separadas. No método de precesión, a cámara é plana e rota arredor dun eixe paralelo ao eixe de rotación do cristal. En ambos os métodos úsase unha pantalla para medir só unha sección bidimensional da rede recíproca en cada imaxe.Modelo:HarvnpModelo:Harvnp Estes métodos facilitan a determinación da orientación do cristal e os índices das reflexións, pero son lentos e ineficientes. Os avances en computación dos anos 90 posibilitaron un deseño máis simple, no que o detector se mantén estacionario detrás do cristal, usándose programas para achar automaticamente a orientación e os parámetros cristalinos consistentes co padrón de difracción observado.

Método do po cristalino

Padrón de difracción de po. Debido ao uso de múltiples cristais en múltiples orientacións os puntos de difracción correspondentes a puntos da rede recíproca á mesma distancia da orixe d únense para formar un anel.

No método do po cristalino ou de Debye-Scherrer, o cristal a analizar é pulverizado de tal maneira que forme un conxunto de microcristais en todas as posibles orientacións da rede recíproca. Con esta xeometría pódense medir todas as reflexións nun só padrón de difracción, consistente en círculos, un para cada reflexión. Aínda que o método de rotación de cristal dá valores máis exactos da intensidade das reflexións, o método de po é ás veces a única opción cando o material a estudar non forma monocristais dun tamaño suficiente para producir difracción detectable. Este método úsase maioritariamente cando non é necesario determinar a estrutura; por exemplo, na análise de minerais presentes nunha mostra.

Aplicacións

A cristalografía ten moitas aplicacións nunha gran variedade de disciplinas científicas, como a mineraloxía, a química, a bioloxía molecular, a farmacoloxía, a xeoloxía, a física aplicada e a ciencia de materiais. Igualmente, as diferenzas no padrón de difracción de diversos materiais, xeo, minerais, fármacos, pigmentos, adsorbentes, catalizadores etc. con aspectos e composicións químicas similares son de moita utilidade na industria e campos sen relación directa coa investigación científica básica ou o desenvolvemento tecnolóxico, como a ciencia forense ou a historia da arte.

Premios Nobel

Cristais de insulina. A cristalografía de proteínas contribuíu notablemente ao desenvolvemento da bioloxía molecular.

Varios dos descubrimentos e avances científicos que se levaron a cabo grazas á cristalografía de raios X foron galardoados co Premio Nobel. Entre eles unha alta proporción concedéronse a descubrimentos en química orgánica e bioloxía; os primeiros foron os dous premios de 1962 a Kendrew e Perutz en Química e Crick, Watson e Wilkins en Medicina, seguidos dous anos máis tarde polo premio a Dorothy Hodgkin. Tras catro décadas de expansión, a cristalografía de macromoléculas empezou a contribuír de maneira significativa ao esclarecemento de moitos procesos clave na bioloxía molecular e celular: En 1997, Boyer, Walker e Skou recibiron o Nobel de Química por dilucidar o mecanismo da síntese do ATP; Roderick MacKinnon obtivo dito premio en 2003 polos seus estudos das canles de potasio na membrana plasmática e Roger Kornberg en 2006 pola análise da maquinaria de transcrición xenética. En 2009, foille outorgado a Ramakrishnan, Steitz e Yonath polo estudo da estrutura e función do ribosoma, complexo celular que realiza a síntese de proteínas, e en 2012 a Lefkowitz e Kobilka pola investigación sobre os receptores acoplados a proteínas G, proteínas que permiten que as células detecten e respondan a cambios no medio que as rodea.

No eido da química inorgánica, a difracción con raios X contribuíu á obtención da estrutura dos boranos, compostos importantes para a síntese química, por cuxo estudo a Academia sueca recompensou a Herbert Brown co Nobel de Química en 1979. Igualmente, a técnica utilizouse para determinar a estrutura dos fulerenos, materiais con interesantes propiedades físicas e químicas. En 1996, Krotro, Smalley e Curl recibiron o premio polo descubrimento destas moléculas.

Noutras ocasións concedéronse premios Nobel por desenvolvementos teóricos e prácticos da técnica mesma, recoñecendo o seu impacto científico; nesta categoría inclúense os premios en Física a Max von Laue e William Henry e Lawrence Bragg, e o de Química de 1936 a Peter Debye e o de 1985 para Hauptman e Karle polo desenvolvemento dos métodos directos para a solución de estruturas cristalinas.

Análise de minerais

A cristalografía de raios X utilízase non só para obter estruturas descoñecidas, senón tamén para determinar a composición de mostras de solos ou minerais, así como para a identificación de metais e outros elementos. Cada substancia mineral forma cristais cunha cela unidade e simetría determinada, que dá lugar a un padrón de difracción característico. A difracción polo método do po é moi utilizada para este tipo de aplicacións por ser sinxelo comparar o espazado entre os aneis de difracción cos valores compilados polo Joint Committee on Powder Diffraction Standars (JCPDS). As proporcións relativas de dous ou máis minerais presentes nunha mesma mostra obtéñense comparando as intensidades das súas respectivas liñas con aquelas de mostras de composición coñecida. Un exemplo desta aplicación é a identificación de minerais arxilosos, a fracción do solo cuxas partículas minerais teñen un tamaño inferior a dous μm.

O vehículo explorador Curiosity, que aterrou en Marte en 2012 para estudar a superficie do planeta, conta entre os seus instrumentos científicos cun difractómetro compacto equipado cun xerador de raios X e un detector de área.En outubro de 2012, transmitiu as primeiras imaxes de difracción, que demostraron a presenza de minerais como o feldespato, piroxeno e olivina no solo marciano, mesturados con material amorfo, a semellanza dos terreos basálticos dos volcáns de Hawai.

Deseño de fármacos

Desde finais do século XX empezáronse a deseñar novos fármacos e medicamentos baseados en inhibidores e substratos naturais de diversas proteínas e encimas involucrados nos ciclos celular e metabólicos. O coñecemento da estrutura da parte da proteína (a forma e a distribución de cargas electrostáticas) que liga estes compostos facilita este proceso, grazas á mellor comprensión das interaccións entre a proteína e o ligando de interese; isto permite concentrarse no deseño de fármacos coas características específicas desexadas. Un dos exemplos máis importantes desta aplicación é o composto vemurafenib, deseñado para bloquear un encima mutante presente no 60 % dos casos de melanoma.

Comparación con outras técnicas de difracción cristalográfica

Debido á dualidade onda-partícula é posible estudar cristais por medio da difracción dun feixe de neutróns ou de electróns, ademais de con raios X. Os primeiros experimentos de difracción por electróns tiveron lugar en 1926 e a difracción de neutróns observouse por vez primeira en 1936. Aínda que os experimentos e a análise de datos obtidos por cristalografía de electróns, neutróns e raios X teñen moito en común, existen algunhas diferenzas debidas aos diferentes modos de interacción coa materia: os electróns interaccionan tanto co núcleo atómico coma cos electróns que o rodean e os factores de estrutura cristalinos son unhas catro ordes de magnitude maiores que os resultantes da dispersión elástica de raios X, o que fai posible o estudo de mostras de menor tamaño con electróns. Os neutróns, á súa vez, son reflectidos só polo núcleo e non os electróns, aínda que estes contribúen indirectamente ao factor de forma atómico pola creación de campos magnéticos; ademais, a interacción da materia con eles é moito máis débil que cos raios X e é necesario usar reactores nucleares para xerar feixes de neutróns o suficientemente intensos para obter difracción cristalina.

Unha vantaxe importante da difracción de electróns é que pode combinarse coas fases obtidas a partir da transformada de Fourier das imaxes do obxecto nun microscopio electrónico. En 1968, David DeRosier e Aaron Klug publicaron un método para reconstruír mapas de densidade electrónica tridimensionais baseados neste principio. Aínda que a mellor resolución espacial destes mapas (arredor de 0,4 nm) é baixa comparada cos valores acadables con raios X ou neutróns, o procedemento pode ser útil en casos onde o problema das fases impide a solución da estrutura por outros métodos. En canto á cristalografía de neutróns, a vantaxe principal é a clara visualización dos átomos de hidróxeno, moi difíciles de detectar con raios X debido a que só posúen un electrón; esta propiedade constitúe unha vantaxe para o estudo daquelas moléculas orgánicas en cuxa función teña un papel importante o intercambio de hidróxeno.

Limitacións

A limitación fundamental da cristalografía de raios X consiste en que só pode aplicarse a substancias susceptibles de formar cristais. Aínda que as técnicas cristalográficas poden utilizarse tamén para determinar a estrutura doutros materiais con periodicidade espacial, como fibras helicoidales (como a do ADN, algúns tipos de virus etc.) e cuasicristais, é imposible estudar gases, líquidos e sólidos desordenados por este método. Ademais, a obtención de cristais non é sempre suficiente para obter a estrutura de interese: as moléculas de tamaño grande, por exemplo, adoitan ser casos difíciles.

Efectos dos raios X nun enlace disulfuro: os átomos de xofre (en laranxa) capturan os fotoelectróns emitidos polos átomos presentes na molécula ao seren excitados polos raios X. Ao reducírense, o enlace entre eles rompe e despráazanse da súa posición orixinal, como indica a desaparición gradual da densidade electrónica ao seu arredor. Isto ten como resultado un modelo errado da estrutura.

Outro límite da técnica está relacionado co tipo de información que proporciona sobre a estrutura: Os modelos obtidos por difracción representan unha media das posicións atómicas para todas as moléculas do cristal; cando a molécula conta con átomos que oscilan entre diferentes conformacións, a densidade electrónica media esténdese sobre a totalidade do espazo que poden ocupar estes átomos e as partes desordenadas da molécula fanse invisibles. Isto representa un serio problema para o estudo de encimas se o sitio activo da molécula (asociada á súa actividade química) presenta unha gran mobilidade; neste caso a determinación das propiedades de materiais biolóxicos in vivo a partir da súa estrutura cristalina é problemática e require métodos de estudo alternativos, como a resonancia magnética nuclear.

As vibracións atómicas tamén limitan a resolución acadable cos datos de difracción, incluso cando as moléculas adoptan a mesma conformación en distintas celas unidade. A resolución do modelo non adoita ser suficiente para determinar o estado de oxidación, posicionar todos os átomos de hidróxeno ou distinguir elementos con números atómicos semellantes. A feble interacción dos raios X cos átomos lixeiros é outra desvantaxe da técnica en aplicacións como a caracterización de nanomateriais.

Finalmente, as propiedades ionizantes dos raios X poden alterar ou destruír as moléculas do cristal durante o experimento. Cando isto acontece, o modelo obtido non reflicte a verdadeira estrutura molecular e pode dar lugar a interpretacións erradas sobre as súas propiedades. Ademais, as distorsións globais da rede cristalina e outros efectos secundarios da irradiación dificultan a obtención das fases. Este problema é grave en cristais de proteínas, que conteñen unha alta proporción de auga e compostos orgánicos doadamente radiolizables, e un gran número de enlaces químicos susceptibles ao ataque polos radicais libres e electróns producidos por dita radiólise. Os experimentos con moléculas biolóxicas adoitan realizarse a temperaturas de Modelo:Nowrap ou menores; isto frea a difusión dos radicais libres, mais non soluciona enteiramente o problema, porque os fotoelectróns excitados polos raios X permanecen móbiles ata o cero absoluto.

Notas e referencias

Bibliografía

• Modelo:Cita libro
• Modelo:Cita libro
• Modelo:Cita libro
• Modelo:Cita libro
• Modelo:Cita libro

Véxase tamén

Outros artigos

• Cristalografía
• Difracción de electróns
• Difracción de neutróns
• Espectroscopia de raios X
• Resonancia magnética nuclear

Ligazóns externas

• Portal de Cristalografía do Consello Superior de Investigacións Científicas de España Modelo:Es
• Unión Internacional de Cristalografía Modelo:En