Aceleración

Gráfico que mostra a variación da velocidade v ao longo do tempo t dun móbil que non cambia de dirección. En cada punto do gráfico v( t), o módulo da aceleración corresponde ao valor da pendente da recta tanxente á curva que pasa por cada punto: a(1), a(2), a(3). Así a(1) é positiva, a(2) é nula e a(3) é negativa.

No baleiro (sen resistencia do aire), os obxectos atraídos pola Terra gañan velocidade a un ritmo constante.

A aceleración é unha magnitude física vectorial que mide a variación da velocidade respecto á variación do tempo. Descrito en termos diferenciais, dada unha función da posición dun móbil respecto ó tempo, a aceleración será a segunda derivada desta función respecto á variable temporal.

No contexto da mecánica vectorial newtoniana represéntase normalmente como $\overrightarrow{a}$ ou $𝐚$ e o seu módulo como $a$. As súas dimensións son $[L\cdot T^{-2}]$. Mídese en m/s² no Sistema Internacional.

A magnitude da aceleración dun obxecto, tal e como a describe a segunda lei de Newton, é o efecto combinado de dúas causas:

• o balance neto de todas as forzas externas que actúan sobre ese obxecto - a magnitude é directamente proporcional a esta forza neta resultante;
• a masa dese obxecto , dependendo dos materiais dos que está feito, a magnitude é inversamente proporcional á masa do obxecto.

Na mecánica newtoniana, para un corpo con masa constante, a aceleración do corpo é proporcional á forza que actúa sobre o mesmo (segunda lei de Newton): Modelo:Ecuación onde F é a forza resultante que actúa sobre o corpo, m é a masa do corpo, e a é a aceleración. A relación anterior é válida en calquera sistema de referencia inercial.

As súas dimensións son $[L\cdot T^{-2}]$. A súa unidade no Sistema Internacional é m/s². Por exemplo, cando un vehículo arrinca estando detido (velocidade cero, nun marco de referencia inercial) e viaxa en liña recta a velocidades crecentes, está a acelerar na dirección da marcha. Se o vehículo vira, prodúcese unha aceleración cara á nova dirección e cambia o seu vector de movemento. A aceleración do vehículo na súa dirección actual de movemento chámase aceleración lineal (ou tanxencial durante os movementos circulares), a reacción que experimentan os pasaxeiros a bordo como unha forza que os empuxa cara a atrás nos seus asentos. Ao cambiar de dirección, a aceleración que efectúa chámase aceleración radial (ortogonal durante os movementos circulares), a reacción que experimentan os pasaxeiros como unha forza centrífuga. Se a velocidade do vehículo diminúe, isto é unha aceleración na dirección oposta e matematicamente negativa, ás veces chamada desaceleración, e os pasaxeiros experimentan a reacción á desaceleración como unha forza inercial que os empuxa cara a adiante. Estas aceleracións negativas a miúdo lógranse mediante a combustión de retrocohetes en naves espaciais. Tanto a aceleración como a desaceleración trátanse da mesma maneira, ambos son cambios de velocidade. Os pasaxeiros senten cada unha destas aceleracións (tanxencial, radial, desaceleración) ata que a súa velocidade relativa (diferencial) neutralízase con respecto ao vehículo.

Enfoque intuitivo

Ilustracións do concepto de aceleración:
1) O movemento non sofre aceleración.
2) A velocidade aumenta constantemente.
3) A velocidade diminúe constantemente.
4) A aceleración describe unha curvatura da traxectoria.

Así como a velocidade describe a modificación da posición dun obxecto no tempo, a aceleración describe a «modificación da velocidade no tempo» (que as matemáticas formalizan coa noción de derivada). Na vida cotiá, hai tres casos que o físico agrupa baixo o concepto único de aceleración:

• ir máis rápido (acelerar no sentido común máis restritivo): nun automóbil, o velocímetro mostra que a velocidade está a aumentar;

desde un punto de vista matemático, a aceleración é positiva, é dicir que o vector de aceleración ten un compoñente na dirección da velocidade;

• ir máis lento (frear, desacelerar ou diminuír a velocidade na linguaxe común): a indicación do velocímetro diminúe;

a aceleración é negativa, ou o vector de aceleración ten un compoñente oposta á dirección da velocidade;

• cambio de dirección (xirar ou virar na linguaxe común): mesmo se a indicación do velocímetro non cambia, o cambio de dirección implica aceleración;

o vector de aceleración ten un compoñente perpendicular á velocidade; aquí interésanos a variación da dirección do vector velocidade, non a variación da súa norma.

Cando unha persoa está sometida a unha aceleración, sente un esforzo: forza que preme contra o asento cando o coche acelera (vai máis rápido), forza que empuxa cara ao parabrisas cando o coche frea, forza que empuxa ao carón cando o coche frea ou está a virar (forza centrífuga). sente esta tensión de maneira similar ao peso. A relación entre aceleración e esforzo é o dominio da dinámica ; pero a aceleración é unha noción de cinemática, é dicir que se define só a partir do movemento, sen involucrar as forzas.

Introdución

En conformidade coa mecánica newtoniana, unha partícula non pode seguir unha traxectoria curva a menos que sobre ela actúe unha certa aceleración, como consecuencia da acción dunha forza, xa que se esta non existise, o seu movemento sería rectilíneo. Así mesmo, unha partícula en movemento rectilíneo só pode cambiar a súa velocidade baixo a acción dunha aceleración na mesma dirección da súa velocidade (dirixida no mesmo sentido se acelera; ou en sentido contrario se desacelera).

Algúns exemplos do concepto de aceleración serían:

• A chamada aceleración da gravidade na Terra é a aceleración que produce a forza gravitatoria terrestre. O seu valor na superficie da Terra é, aproximadamente, de 9,8 m/s². Isto quere dicir que se se deixara caer libremente un obxecto, aumentaría a súa velocidade de caída a razón de 9,8 m/s por cada segundo (sempre que omitamos a resistencia aerodinámica do aire). O obxecto caería, polo tanto, cada vez máis rápido, respondendo dita velocidade a ecuación:

• Unha manobra de freado dun vehículo, que se correspondería cunha aceleración de signo negativo, ou desaceleración, ao opoñerse á velocidade que xa tiña o vehículo. Se o vehículo adquirise máis velocidade, dito efecto chamaríase aceleración e, neste caso, sería de signo positivo.

Aceleración en cinemática puntual

O caso máis común

Aceleración e cantidades relacionadas

O vector de aceleración dun punto material en calquera momento atópase mediante unha diferenciación temporal única do vector velocidade dun punto material (ou diferenciación dobre do vector radio)

$\overrightarrow{a}=\frac{d\overrightarrow{v}}{dt}=\frac{d^2\overrightarrow{r}}{d{t}^2}.$

Se se coñecen as coordenadas do punto na traxectoria $\overrightarrow{r}(t_0)={\overrightarrow{r}}_0$ e o vector de velocidade $\overrightarrow{v}(t_0)={\overrightarrow{v}}_0$ en calquera momento do tempo Modelo:Math, así como a dependencia da aceleración no tempo $\overrightarrow{a}(t),$ ao integrar esta ecuación, pódense obter as coordenadas e a velocidade do punto en calquera momento do tempo Modelo:Math (tanto antes como despois do momento Modelo:Math)

$\overrightarrow{v}(t)={\overrightarrow{v}}_0+\underset{t_0}{\overset{t}{\int }}\overrightarrow{a}(\tau )d\tau ,$

$\overrightarrow{r}(t)={\overrightarrow{r}}_0+(t-t_0){\overrightarrow{v}}_0+\underset{t_0}{\overset{t}{\int }}\underset{t_0}{\overset{\xi }{\int }}\overrightarrow{a}(\tau )d\tau d\xi .$

A derivada temporal da aceleración, é dicir, o valor que caracteriza a taxa de cambio na aceleración, chámase arrancada:

$\overrightarrow{j}=\frac{\mathrm{d}\overrightarrow{a}}{\mathrm{d}t},$ onde $\overrightarrow{j}$ — é o vector da arrancada.

Aceleración media e instantánea

Definición da aceleración dunha partícula nun movemento calquera. Obsérvese que a aceleración non é tanxente á traxectoria.

Cada instante, ou sexa, en cada punto da traxectoria, queda definido un vector velocidade que, en xeral, cambia tanto en módulo como en dirección ao pasar dun punto a outro da traxectoria. A dirección da velocidade cambiará debido a que a velocidade é tanxente á traxectoria e esta, polo xeral, non é rectilínea. Na Figura represéntanse os vectores velocidade correspondentes aos instantes t e t+Δt, cando a partícula pasa polos puntos P e Q, respectivamente. O cambio vectorial na velocidade da partícula durante ese intervalo de tempo está indicado por Δv, no triángulo vectorial ao pé da figura. Defínese a aceleración media da partícula, no intervalo de tempo Δt, como o cociente: Modelo:Ecuación

que é un vector paralelo a Δv e dependerá da duración do intervalo de tempo Δt considerado. A aceleración instantánea defínese como o límite ao que tende o cociente incremental Δv/Δt cando Δt→0; isto é, a derivada do vector velocidade con respecto ao tempo: Modelo:Ecuación

Posto que a velocidade instantánea v á súa vez é a derivada do vector posición r respecto ao tempo, a aceleración é a derivada segunda da posición con respecto do tempo: Modelo:Ecuación

De igual forma pódese definir a velocidade instantánea a partir da aceleración como: Modelo:Ecuación

Pódese obter a velocidade a partir da aceleración mediante integración: Modelo:Ecuación

Medición da aceleración

A medida da aceleración pode facerse cun sistema de adquisición de datos e un simple acelerómetro. Os acelerómetros electrónicos son fabricados para medir a aceleración nunha, dúas ou tres direccións. Contan con dous elementos condutivos, separados por un material que varía a súa condutividade en función das medidas, que á súa vez serán relativas á aceleración do conxunto.

Unidades

As unidades da aceleración son:

• Sistema Internacional

1 m/s²

• Sistema Ceguesimal

1 cm/s² = 1 Gal

Modelo:Nowrap

	м/с²	pé/с²	Modelo:Math	см/с²
1 м/с² =	1	3,28084	0,101972	100
1 Pie/с² =	0,304800	1	0,0310810	30,4800
Modelo:Math =	9,80665	32,1740	1	980,665
1 см/с² =	0,01	0,0328084	0,00101972	1

Valores de aceleración nalgúns casos

Valores das aceleracións de varios movementos:

Tipo de movemento	Aceleración, m/s²
Aceleración centrípeta do sistema solar orbitando a galaxia	2,2×10-10
0,0060
Aceleración centrípeta da Lúa que orbita ao redor da Terra	0,0027
Ascensor de pasaxeiros	0,9-1,6
Tren metro	1
Coche Zhiguli	1,5
Corredor de curta distancia	1,5
Ciclista	1.7
Patinador sobre xeo	- 1.9
Motocicleta	3-6
Freado de emerxencia do coche	4-6
Usain Bolt, aceleración máxima	8.
Coche de carreiras	8-9
Freado ao abrir o paracaídas	30 (3 Modelo:Math)
Lanzamento e desaceleración de nave espacial	40-60 (4-6 Modelo:Math)
Manobra dun avión de reacción	ata 100 (ata 10 Modelo:Math)
Estaca despois do impacto dun bate estacas	300 (30 Modelo:Math)
Pistón motor de combustión interna	3×10³
Bala no canón dun rifle	2,5×105
Micropartículas no acelerador	(2-50)×1014
Electrón entre o cátodo e o ánodo no tubo de raios catódicos dunha televisión en cor con (20Modelo:EsdkV, 0,5Modelo:Esdm)	≈7×1015
Electróns ao impactar con fósforo no tubo dun televisor en cor (20 kV)	≈1022
Partícula alfa no núcleo atómico	≈1027

Nota: aquí Modelo:Math ≈ 10Modelo:Esdm/s².

Compoñentes intrínsecos da aceleración: aceleración tanxencial e aceleración normal

Compoñentes intrínsecos da aceleración.

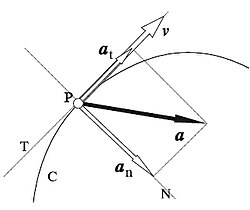
En tanto que o vector velocidade v é tanxente á traxectoria, o vector aceleración a pode descompoñerse en dous compoñentes (chamados compoñentes intrínsecos) mutuamente perpendiculares: un compoñente tanxencial a_t (na dirección da tanxente á traxectoria), chamado aceleración tanxencial, e un compoñente normal a_n (na dirección da normal principal á traxectoria), chamado aceleración normal ou centrípeta (este último nome en razón a que sempre está dirixida cara ao centro de curvatura).

Derivando a velocidade con respecto ao tempo, tendo en conta que o vector tanxente cambia de dirección ao pasar dun punto a outro da traxectoria (isto é, non é constante) obtemos Modelo:Ecuación sendo ${\widehat{𝐞}}_t$ o vector unitario tanxente á traxectoria na mesma dirección que a velocidade e $\mathit{\omega }$ a velocidade angular. Resulta conveniente escribir a expresión anterior na forma Modelo:Ecuación sendo

${\widehat{𝐞}}_n$ o vector unitario normal á traxectoria, isto é, dirixido cara ao centro de curvatura da mesma,

$\rho$ o raio de curvatura da traxectoria, isto é, o raio da circunferencia osculatriz á traxectoria.

As magnitudes destes dous compoñentes da aceleración son: Modelo:Ecuación Cada un destes dous compoñentes da aceleración ten un significado físico ben definido. Cando unha partícula se move, a súa velocidade pode cambiar e este cambio mídeo a aceleración tanxencial. Pero se a traxectoria é curva tamén cambia a dirección da velocidade e este cambio mídeo a aceleración normal.

• Se no movemento curvilíneo a velocidade é constante (v=cte), a aceleración tanxencial será nula, pero haberá unha certa aceleración normal, de modo que nun movemento curvilíneo sempre haberá aceleración.
• Se o movemento é circular, entón o raio de curvatura é o raio R da circunferencia e a aceleración normal escríbese como a_n = v²/R.
• Se a traxectoria é rectilínea, entón o raio de curvatura é infinito (ρ→∞) de modo que a_n=0 (non hai cambio na dirección da velocidade) e a aceleración tanxencial a_t será nula ou non segundo a velocidade sexa ou non constante.

Os vectores que aparecen nas expresións anteriores son os vectores do triedro de Frênet que aparece na xeometría diferencial de curvas do seguinte xeito:

${\widehat{𝐞}}_t$ é o vector unitario tanxente á curva.

${\widehat{𝐞}}_n$ é o vector unitario normal á curva.

$\mathit{\omega }$ é o vector velocidade angular que é paralelo ao vector binormal á curva.

Movemento circular uniforme

Cinemática do movemento circular.

Modelo:Artigo principal Un movemento circular uniforme é aquel no que a partícula percorre unha traxectoria circular de raio R con velocidade constante, é dicir, que a distancia percorrida en cada intervalo de tempo igual é a mesma. Para ese tipo de movemento o vector de velocidade mantén o seu módulo e vai variando a dirección seguindo unha traxectoria circular. Se se aplican as fórmulas anteriores, tense que a aceleración tanxencial é nula e a aceleración normal é constante: esta aceleración normal chámase "aceleración centrípeta". Neste tipo de movemento a aceleración simplemente modifica a traxectoria do obxecto e non a súa velocidade. Modelo:Ecuación

Movemento rectilíneo acelerado

No Movemento Rectilíneo Acelerado, a aceleración instantánea queda representada como a pendente da recta tanxente á curva que representa graficamente a función v(t).

Se se aplican as fórmulas anteriores ao movemento rectilíneo, no que só existe aceleración tanxencial, ao estar todos os vectores contidos na traxectoria, podemos prescindir da notación vectorial e escribir simplemente: Modelo:Ecuación Xa que nese tipo de movemento os vectores $𝐚$ e $𝐯$ son paralelos, satisfacendo tamén a relación: Modelo:Ecuación As coordenadas de posición veñen dada neste caso por: Modelo:Ecuación Un caso particular de movemento rectilíneo acelerado é o movemento rectilíneo uniformemente acelerado, onde a aceleración é ademais constante e polo tanto, a velocidade e as coordenadas de posición veñen dadas por: Modelo:Ecuación

Aceleración en mecánica relativista

Relatividade especial

O análogo da aceleración en mecánica relativista chámase cuadriaceleración e é un cuadrivector cuns tres compoñentes espaciais que para pequenas velocidades coinciden cos da aceleración newtoniana (o compoñente temporal para pequenas velocidades resulta proporcional á potencia da forza divida pola velocidade da luz e a masa da partícula).

En mecánica relativista a cuadrivelocidade e a cuadriaceleración son sempre ortogonais, iso vén de que a cuadrivelocidade ten un (pseudo)módulo constante: Modelo:Ecuación onde c é a velocidade da luz e o produto anterior é o produto asociado á métrica de Minkowski: Modelo:Ecuación

Relatividade xeral

Na teoría xeral da relatividade o caso da aceleración é máis complicado, xa que debido a que o propio espazo-tempo é curvo (ver curvatura do espazo-tempo), unha partícula sobre a que non actúa ningunha forza pode seguir unha traxectoria curva, de feito a liña curva que segue unha partícula sobre a que non actúa ningunha forza exterior é unha liña xeodésica, de feito en relatividade xeral a forza gravitatoria non se interpreta como unha forza senón como un efecto da curvatura do espazo-tempo que fai que as partículas non sigan traxectorias rectas senón liñas xeodésicas. Neste contexto a aceleración non xeodésica dunha partícula é un vector cuxos catro compoñentes se calulan como: Modelo:Ecuación Aquí $\alpha =0,1,2,3$ (compoñente temporal e tres compoñentes espaciais). Apréciase que cando os símbolos de Christoffel ${\mathrm{\Gamma }}_{\beta \gamma }^{\alpha }$ unha partícula pode ter aceleración cero aínda que o seu cuadrivelocidade non sexa constante, iso sucede cando a partícula segue unha liña xeodésica dun espazo-tempo de curvatura non nula.

Importancia da aceleración na enxeñería mecánica

A enxeñería mecánica é o deseño e fabricación de máquinas, é dicir, sistemas que realizan movementos. Unha parte importante é o dimensionamento, é dicir a elección de actuadores (gatos, motores) e pezas que soportan as forzas. Se as masas postas en movemento e/ou as aceleracións son grandes, os efectos dinámicos -as forzas necesarias para crear as aceleracións, ou as forzas resultantes das aceleracións- non son desprezables. Xa que logo, determinar a aceleración instantánea durante un movemento é fundamental para que as pezas resistan e para determinar o consumo enerxético do sistema. Modelo:Cita

En moitos casos, a especificación é "levar un obxecto do punto A ao momento B nun tempo t, co tempo t ás veces expresado como unha taxa (realizando o movemento n veces por hora). O deseño consiste en :

1. Elixir unha solución tecnolóxica para guiar o movemento, xa sexa nos casos simples:
   • Traslado rectilíneo guiado por un elo deslizante ou equivalente (sistema de raíles/rodetes), o máis sinxelo de imaxinar, pero potencialmente suxeito o arrastre;
   • movemento circular de translación (se o obxecto debe manter a mesma orientación, tipicamente cun paralelogramo deformable) ou movemento de rotación, simple de imaxinar, e xeralmente máis interesante (elo pivotante son xeralmente máis baratos e máis robustos que os elos deslizantes), pero cunha traxectoria máis grande (polo tanto require unha maior velocidade, e máis espazo libre) ;
   • Traslado pseudo rectilíneo, por exemplo co paralelogramo de Watt, combinando a vantaxe de ambos os (ligazóns pivotantes robustos e baratos, traxectoria curta e compacta);
   • Traxectoria máis complexa, segundo requírase (guiado por carril ou leva, brazo robótico).
2. Elixe unha solución tecnolóxica para crear o movemento ( actuador), controlalo (automatismo, leva) e transmitilo (transmisión).
3. En función da traxectoria (polo tanto a solución tecnolóxica de guiado), determinar as leis do movemento para cumprir as especificacións (duración do movemento admisible) aforrando as pezas (limitación dos esforzos e, xa que logo, da aceleración) e o consumo de enerxía (limitación das aceleracións e da velocidade, ver os artigos Traballo dunha forza e Fricción).
4. Segundo as leis do movemento, determinar a poder necesaria, e as forzas ás que están sometidas as partes.
5. Dimensionar o sistema: elixir as pezas dos catálogos do provedor, ou deseñalas (elixir os materiais, as dimensións, debuxalas).

Véxase tamén

Bibliografía

• Modelo:Cita libro
• Modelo:Cita libro
• Modelo:Cita libro
• Modelo:Cita libro
• Modelo:Cita libro
• Landau L.D., Lifshits E.M. «Mechanics». Edición 5, estereotipada. M.: Fizmatlit, 2004. 224Modelo:Esdpp. (Física Teórica, volumeModelo:EsdI). ISBN 5-9221-0055-6.
• David C. Cassidy, Gerald James Holton e F. James Rutherford. Comprensión de la física. Birkhäuser (inglés) ruso, 2002. ISBN 978-0-387-98756-9.
• Pauli W. Teoría de la relatividad. Dover, 1981. ISBN 978-0-486-64152-2.
• Michel Combarnous, Didier Desjardins e Christophe Bacon, Mecánica de sólidos y sistemas de sólidos, Dunod, coll.Modelo:Esd«Ciencias superiores», 2004, 3 e ed. ISBN 978-2-10-048501-7, pp.Modelo:Esd25, 35-37, 38-40, 99-103.
• Jean-Louis Fanchon, guía mecánico, Nathan, 2001. ISBN 978-2-09-178965-1, pp.Modelo:Esd134-135, 143-145, 153-154, 166-168, 180-181, 193-194.

Outros artigos

• Cinemática
• Velocidade
• Derivada

Ligazóns externas

• Serie de vídeos explicativos sobre a aceleración en caída libre no YouTube Modelo:Es
• Acceleration and free fall Modelo:Webarchive - a chapter from an online textbook (en inglés)
• Science aid: Movement Modelo:En
• Science.dirbix: Acceleration Modelo:En
• Acceleration Calculator Modelo:En