Triángulo de Pascal

O triángulo de Pascal, tamén coñecido como triángulo de Tartaglia, é un triángulo de números enteiros, infinito e simétrico.

Fundamentos

Constrúese do seguinte xeito:

Empézase polo «1» do cume. Dunha liña á seguinte convén escribir os números cun desfasamento de media casa. Así, as casas (que non se debuxan) terán cada unha dúas casas xusto encima, na liña anterior. O valor que se escribe nunha casa é a suma dos valores das dúas casas enriba dela. O valor cero non se escribe. Por exemplo, na última liña debuxada, o cuarto valor é 84 = 28 + 56, suma do terceiro e cuarto valor da liña anterior.

Obsérvase, e non é difícil demostralo, que a diagonal exterior está formada de uns, a segunda diagonal dos naturais en orde crecente, que os números non fan máis que aumentar dunha liña á seguinte e que existe un eixo de simetría vertical que pasa polo vértice.

Con todo, o interese deste triángulo non radica nestas propiedades, senón no vínculo que ten coa álxebra elemental. En efecto, as cifras 1; 2; 1 e 1; 3; 3; 1 recordan as identidades:

(a + b)^{2} = a^{2} + 2 a b + b^{2}

(a + b)^{3} = a^{3} + 3 a^{2} b + 3 a b^{2} + b^{3}

pois son os coeficientes dos seus monomios. Este parecido non é casual e xeneralízase a calquera potencia do binomio a + b.

Fórmula

No triángulo de Pascal, cada número é a suma dos dous números directamente enriba del.

Na

n

-ésima fila do triángulo de Pascal, a entrada na posición

k

denótase como

(\binom{n}{k})

, e pronúnciase como Modelo:Mvar sobre Modelo:Mvar. Por exemplo, a entrada máis alta é

(\binom{0}{0}) = 1

. Con esta notación, a construción do parágrafo da introdución pode escribirse como

(\binom{n}{k}) = (\binom{n - 1}{k - 1}) + (\binom{n - 1}{k})

para calquera número enteiro positivo $n$ e calquera número enteiro $0 \leq k \leq n$ .^[1] Esta recorrencia para os coeficientes binomiais coñécese como Regra de Pascal.

Relación entre o triángulo de Pascal e o binomio de Newton

A fórmula que dá o desenvolvemento de $(a + b)^{n}$ segundo as potencias crecentes de a (e decrecentes de b) chámase binomio de Newton. Nesta expresión, o único que se descoñece son os coeficientes dos monomios $a^{k} b^{n - k}$ .

Teorema

Os coeficientes da forma desenvolvida de (a + b)ⁿ son dados
pola liña número n+1 do triángulo de Pascal (a que empeza por 1 e n).

Proba

Xa está visto que é certo para n=2 e n=3. Tamén o é para n=0.
Para establecer o resultado para calquera valor de n ∈ ℕ, o máis natural é proceder por indución. Supondo que é certo para un valor de n, hai que deducir que o é tamén para n+1. No canto de facelo no caso xeral (sería pouco claro) miremos que sucede ao pasar da liña n = 3 á liña n = 4.

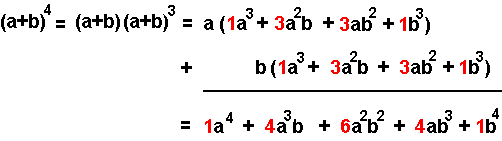
Como mostra a figura, o desenvolvemento de (a + b)⁴ consiste en dúas copias do desenvolvemento de (a + b)³. Están desfasadas (unha corresponde a a⋅(a + b)³ e a outra a b⋅(a + b)³) e cando se suman, un mesmo coeficiente aparece nunha posición dada e outra vez un paso á dereita.
Se se consideran só os coeficientes, inscritos en sendas casas, obtemos a suma seguinte:

e obviamente non fai falta escribir dúas veces as mesmas cifras: a suma consiste en engadir a un coeficiente o coeficiente inmediatamente á súa dereita (o 1 co 3, o 3 co segundo 3 etc) e isto é xustamente o que se fai no triángulo de Pascal. Noutras palabras, o triángulo simula a multiplicación de (a + b), dunha liña á seguinte.

Coeficientes do binomio de Newton

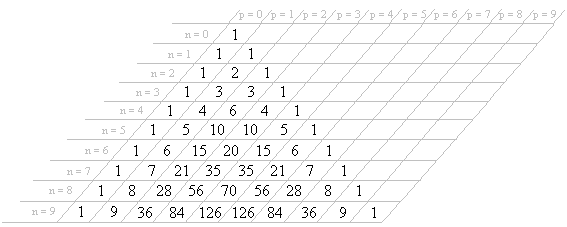
Inscríbese o triángulo de Pascal nunha táboa para poder nomear a cada coeficiente do mesmo. O número na liña n e a columna k (que na figura aparecen como as antidiagonais con letra p) denótase:

(\binom{n}{k})

ou máis raramente

C_{n}^{k}

ou

C (n, k) .

("C" por "combinación") (por exemplo en calculadoras de peto, como a TI-86 e familia), e dise "n sobre k", "combinación de n en k" moito máis curto que "coeficiente binomial n, k". As casas baleiras corresponden a valores nulos. Por definición mesma, temos, (para todo n natural):

(a + b)^{n} = \sum_{k = 0}^{n} (\binom{n}{k}) a^{n - k} b^{k}

para calquera valor de a e b. De feito, é unha igualdade de polinomios en $ℤ [a, b]$ . Sen perder en xeneralidade, resulta ás veces máis práctica a "definición" :

(x + 1)^{n} = \sum_{k = 0}^{n} (\binom{n}{k}) x^{k}

vista como unha igualdade de polinomios en $ℤ [x]$ . Desta fórmula dedúcense dúas consecuencias:

Tomando $x = 1$ obtense: $\sum_{k = 0}^{n} (\binom{n}{k}) = 2^{n}$

A suma dos coeficientes dunha mesma liña vale 2ⁿ. En efecto: 1 = 2⁰, 1 + 1 =2= 2¹, 1 + 2 + 1 =4= 2², 1 + 3 + 3 + 1 =8= 2³, 1 + 4 + 6 + 4 + 1 =16= 2⁴ ... ·

Tomando $x = - 1$ obtense, (para n > 0): $\sum_{k = 0}^{n} (\binom{n}{k}) (- 1)^{k} = 0$

a suma alterna dos números dunha mesma liña vale 0.

En efecto: 1 - 1 = 0, 1 - 2 + 1 = 0, 1 - 3 + 3 - 1 = 0, 1 - 4 + 6 - 4 + 1 = 0, 1 - 5 + 10 - 10 + 5 - 1 = 0 ...

As propiedades que observamos no triángulo pódense agora escribir con todo rigor (ter en conta de novo que usualmente úsase a letra k para a columna que aparece na figura como p):

.

(\binom{n}{0}) = (\binom{n}{n}) = 1

(antidiagonal esquerda e diagonal da dereita do triángulo).

.

(\binom{n}{1}) = (\binom{n}{n - 1}) = n

(segundas diagonal e antidiagonal).

.

(\binom{n}{n - k}) = (\binom{n}{k})

(simetría respecto ao eixo vertical do triángulo).

.

(\binom{n}{k}) = 0

cando k > n (corresponde á zona que está fóra do triángulo).

E claro, a regra de construción do triángulo dá a relación fundamental dos coeficientes binomiais (escrita comezando cos sumandos no índice da fila inferior, mentres que no apartado da fórmula escríbese comezando co resultado do índice da fila superior):

.

$(\binom{n}{k}) + (\binom{n}{k + 1}) = (\binom{n + 1}{k + 1})$

Diagonais

Modelo:Pascal triangle simplex numbers.svg As diagonais do triángulo de Pascal conteñen os números figurados dos simplex:

As diagonais que van polos lados esquerdo e dereito só conteñen 1.
As seguintes diagonais ás laterais conteñen os números naturais en orde.
Movéndose cara a dentro, o seguinte par de diagonais conteñen os números triangulares en orde.
O seguinte par de diagonais contéñen os números tetraédricos en orde, e o seguinte par dá os números do pentatopo.

En xeral

\begin{matrix} P_{0} (n) & = P_{d} (0) = 1, \\ P_{d} (n) & = P_{d} (n - 1) + P_{d - 1} (n) \\ = \sum_{i = 0}^{n} P_{d - 1} (i) = \sum_{i = 0}^{d} P_{i} (n - 1) . \end{matrix}

Unha fórmula alternativa que non implica recursión é

P_{d} (n) = \frac{1}{d!} \prod_{k = 0}^{d - 1} (n + k) = \frac{n^{(d)}}{d!} = (\binom{n + d - 1}{d}),

onde n^(d) é o factorial ascendente.

Interpretación en combinatoria

Os coeficientes binomiais son a base mesma da combinatoria. Vexamos o porqué:

Tomemos de novo un binomio, por exemplo $(a + b)^{3}$ , e desenvolvémolo, pero dun xeito distinto do parágrafo anterior:

(a + b)^{3} = (a + b) \cdot (a + b) \cdot (a + b)

agora quitemos o paréntese, pero sen mudar a orde nos produtos, é dicir sen aplicar a conmutatividade:

(a + b) \cdot (a + b) \cdot (a + b) = (a a + a b + b a + b b) \cdot (a + b)

= a a a + a a b + a b a + a b b + b a a + b a b + b b a + b b b

E agrupemos os termos que conteñen o mesmo número de a, (e de b):

= a a a + (a a b + a b a + b a a) + (a b b + b a b + b b a) + b b b

A primeira paréntese contén todas as palabras constituídas dun b e dous a. Neste caso, é fácil ver que hai exactamente tres. No caso xeral, para contar as palabras, hai que aplicar a conmutatividade, pois as palabras que conteñen o mesmo número de a e de b darán o mesmo termo:

= 1 \cdot a^{3} + 3 \cdot a^{2} b + 3 \cdot a b^{2} + 1 \cdot b^{3}

O primeiro factor 3, que é

(\binom{3}{1})

conta as tres palabras mencionadas (aab, aba e baa).

O segundo factor 3, que é

(\binom{3}{2})

conta as palabras feitas de dous b e un a (abb, bab e bba).

Obviamente, só hai unha palabra de tres letras constituídas de a soamente, e isto corresponde ao monomio 1·a³, con 1 = $(\binom{3}{0})$ («0» por ningunha b).

No canto de falar de palabras formadas con a e b, é equivalente imaxinar unha fileira de n caixóns inicialmente baleiros, e p bólas intercambiables que se teñen que repartir, en cada caixón non cabendo máis dunha. Trátase en todos os casos de repartir p obxectos entre n sitios posibles, ou de escoller un grupo de p obxectos/sitios entre n obxectos/sitios. De aí a apelación p entre n.

Todo o anterior leva ao teorema:

Hai exactamente

(\binom{n}{p})

xeitos de escoller un conxunto de p elementos entre n elementos.

En matemática formal, prefírese falar de conxuntos:

Existen

(\binom{n}{p})

subconxuntos de cardinal p nun conxunto de cardinal n.

Este punto de vista permite achar a fórmula para os coeficientes binomiais. En efecto, para elixir o «primeiro» elemento, hai n posibilidades, logo para escoller o segundo quedan n-1 posibilidades e así sucesivamente ata o elemento número p, que ten n-p+1. A orde no que se escolleron estes p elementos non importa, podíase obter o mesmo subconxunto de p elementos noutra orde. Hai p! permutacións posibles destes p elementos, é dicir p! xeitos de obter o mesmo conxunto.

Xa que logo hai

\frac{n \cdot (n - 1) \cdot (n - 2) . . . (n - p + 1)}{p!}

subconxuntos posibles.

En conclusión:

$(\binom{n}{p}) = \frac{n \cdot (n - 1) \cdot (n - 2) . . . (n - p + 1)}{p \cdot (p - 1) \cdot (p - 2) . . . 2 \cdot 1} = \frac{n!}{p! \cdot (n - p)!}$

Verifiquémolo nun exemplo:

(\binom{5}{2}) = \frac{5!}{2! 3!} = \frac{5 \times 4 \times 3 \times 2}{2 \times 3 \times 2} = 10

No triángulo, o valor na quinta liña e segunda columna é 10. Para rematar, listemos as palabras de cinco letras formadas de 2 a e 5-2 = 3 b (na orde alfabética, ou na orde crecente considerando que a é a cifra 0 e b a cifra 1):
aabbb, ababb, abbab, abbba, baabb, babab, babba, bbaab, bbaba, bbbaa.

A fórmula permite verificar todas as propiedades do parágrafo anterior, con todo pódese prescindir dos cálculos na maioría dos casos, con tal de manipular os conceptos idóneos.

Un subconxunto A de E define unha partición de E en dúas partes E = A ∪ B, con A ∩ B = {} = ∅ (conxunto baleiro). Aquí $B = \overline{A}$ é o complementario de A en E.

Dá o mesmo escoller os p elementos de A que os n-p elementos de $\overline{A}$ .

Isto xustifica, sen cálculo, a simetría

(\binom{n}{n - p}) = (\binom{n}{p})

.

Se p > n, non hai subconxuntos de E con p elementos, porque E contén só n, logo

(\binom{n}{p}) = 0

Tamén son evidentes as igualdades

(\binom{n}{1}) = n

e

(\binom{n}{0}) = 1

porque, no primeiro caso,

hai tantos xeitos de escoller subconxuntos de tamaño 1 que de elementos de E, e no segundo caso, só existe un conxunto con cero elementos: o conxunto baleiro.

A regra fundamental tamén ten explicación gráfica:

Proba: escóllese un elemento e calquera de E, que contén n+1 elementos: E = E' ∪ {e}. Logo considéranse os subconxuntos A de E de cardinal p+1. Son de dous tipos: ou conteñen e, ou non.

Se e ∈ A, entón falta elixir p elementos de E' para completar A. Hai

(\binom{n}{p})

posibilidades.

Se e ∉ A, entón falta elixir p+1 elementos de E' para definir A. Hai

(\binom{n}{p + 1})

posibilidades.

Sumando os dous casos, obtense todas as partes de p+1 elementos de E, constituído de n+1 elementos.

Hai xa que logo

(\binom{n + 1}{p + 1}) = (\binom{n}{p + 1}) + (\binom{n}{p})

Un exemplo:

Aquí vai unha propiedade aritmética, sen interpretación xeométrica: cando n é primo, os coeficientes binomiais na liña n son divisibles por n, excepto os dous bordos da mesma (que valen 1). Escrito formalmente:

Teorema :

\forall p \in [1; n - 1], n / (\binom{n}{p})

Na figura, os exemplos están en verde, e os contraexemplos (cando n non é primo e p divide n) en amarelo.

Proba: na fracción

\frac{n!}{p! (n - p)!}

o factor primo

n aparece unha vez no numerador e xamais no denominador. (O denominador é un produto de números entre 1 e n-1). Xa que logo a fracción é divisible por n.

Xeneralización

No canto de considerar as potencias de a + b, pódese mirar as do trinomio a + b + c.

(a + b + c)ⁿ é unha suma de monomios da forma λ_{p, q, r} ·a ^p·b^q·c^r, con p, q e r positivos, p + q + r = n, e λ_{p, q, r} un natural que se tería que chamar coeficiente trinomial.

Os cálculos son similares aos do coeficiente binomial, e dan a expresión seguinte:

$λ_{p, q, r} = \frac{n!}{p! q! r!}$

Corresponde ao número de partición en tres dun conxunto de n elementos, en subconxuntos de p, q e r elementos. Un exemplo:

Estes coeficientes pódense achar na analoxía tridimensional do triángulo de Pascal: Poderíase chamar a pirámide de Pascal, é tamén infinita, con seccións triangulares, e o valor en cada casa é a suma dos valores das tres casas encima dela.

Debuxáronse as primeiras seccións a partir do cume.

Obsérvase unha invariante por rotación de 120 graos ao redor dun eixo vertical que pasa polo vértice.

O triángulo de Pascal aparece nas tres caras da pirámide.

Está claro que todo isto pódese xeneralizar a calquera dimensión finita, pero sen a posibilidade de facer debuxos explicativos.

Notas

Modelo:Reflist

Véxase tamén

Modelo:Commonscat

Bibliografía

Outros artigos

Coeficiente binomial.

Modelo:Control de autoridades

↑ O coeficiente binomial $(\binom{n}{k})$ Estabelécese convencionalmente en cero se k é menor que cero ou maior que n.

[1] O coeficiente binomial $(\binom{n}{k})$ Estabelécese convencionalmente en cero se k é menor que cero ou maior que n.

[1]

Triángulo de Pascal

Índice

Fundamentos

Fórmula

Relación entre o triángulo de Pascal e o binomio de Newton

Coeficientes do binomio de Newton

Diagonais

Interpretación en combinatoria

Xeneralización

Notas

Véxase tamén

Bibliografía

Outros artigos

Menú de navegación

Triángulo de Pascal

Fundamentos

Fórmula

Relación entre o triángulo de Pascal e o binomio de Newton

Coeficientes do binomio de Newton

Diagonais

Interpretación en combinatoria

Xeneralización

Notas

Véxase tamén

Bibliografía

Outros artigos

Menú de navegación

Procura