Trigonometría

Expresión gráfica das funcións trigonométricas.

A trigonometría estuda as relacións entre os lados e os ángulos dun triángulo e, por extensión, as propiedades dos puntos (baricentro, circuncentro, incentro e ortocentro) e rectas (mediana, altura, mediatriz e bisectriz) notábeis dun triángulo.

A palabra deriva do grego trigonon (tri', tres e gonia ángulos), triángulo, e metron, medida; é dicir, etimoloxicamente trigonometría é a medida de tres ángulos ou medida de triángulos.

Funcións directas principais

Modelo:Ap En concreto, a trigonometría establece varias funcións trigonométricas para un ángulo, definibles graficamente segundo unha circunferencia de raio unidade de tal xeito que o devandito ángulo ten o seu vértice no centro do círculo (na figura, o ángulo abrangue a zona gris):

Funcións trigonométricas directas

• a función chamada seno dun ángulo (abreviada sen ou sin en LaTeX) relaciona o valor do cateto oposto ó ángulo co da hipotenusa. Polo tanto tomando coma referencia a circunferencia de raio unidade da figura, se a hipotenusa ten valor 1 (o do raio), o seno será o segmento vermello, é dicir, o seno terá o valor do cateto oposto cando a hipotenusa vale a unidade;

$\sin \alpha =\frac{catetooposto}{hipotenusa}$

• a función chamada coseno dun ángulo (abreviada cos, inda que en portugués se escriba con dobre s) relaciona o valor do cateto contiguo (ou adxacente) co da hipotenusa. Na figura, para unha hipotenusa unitaria (o raio), o coseno será o segmento verde, é dicir, o coseno terá o valor do cateto contiguo cando a hipotenusa vale a unidade;

$\cos \alpha =\frac{catetoadxacente}{hipotenusa}$

• a función chamada tanxente (abreviada tan, inda que exista unha tendencia a notala como tg, seguindo e segundo a súa grafía en latín, castelán e inglés) relaciona as dúas anteriores: é dicir, é a relación entre o seno e o coseno. Para facer que o coseno teña valor unitario, faise coincidir co raio, e polo tanto a tanxente é o segmento azul, exterior á circunferencia, é dicir, a tanxente terá o valor do cateto oposto cando o cateto contiguo vale a unidade:

$\tan \alpha =\frac{\sin \alpha }{\cos \alpha }=\frac{catetooposto}{catetoadxacente}=\frac{\frac{catetooposto}{hipotenusa}}{\frac{catetoadxacente}{hipotenusa}}$

O nome destas funcións procede de que estes segmentos marcados están no interior (no seo, para seno e coseno) ou na tanxente á circunferencia de raio unidade.

Funcións directas secundarias (recíprocas ou inversas multiplicativas)

Modelo:Ap Existen outras tres funcións trigonométricas que teñen o valor inversamente proporcional ás tres anteriores. Os seus nomes son secante, cosecante e cotanxente. Os seus nomes tamén proceden da posición do segmento en relación á circunferencia unidade. Estas inversas son (na figura, o ángulo abrangue tamén a mesma zona gris):

Funcións trigonométricas recíprocas ou inversas multiplicativas

• a función chamada secante dun ángulo (abreviada sec) relaciona o valor da hipotenusa co do cateto continuo ó angulo. Polo tanto tomando coma referencia a circunferencia de raio unidade da figura, se o cateto contiguo ten valor 1 (o do raio), a secante será o segmento en trazos verdes, é dicir, a secante terá o valor da hipotenusa cando o cateto contiguo vale a unidade;

$\sec \alpha =\frac{hipotenusa}{catetoadxacente}=\frac{1}{\cos \alpha }$

• a función chamada cosecante dun ángulo (abreviada cosec ou csc nas fórmulas LaTeX) relaciona o valor da hipotenusa co do cateto oposto. Na figura, para un cateto unitario de valor igual ó raio, a cosecante será o segmento en trazos vermellos, é dicir, a cosecante terá o valor da hipotenusa cando o cateto oposto vale a unidade;

$\csc \alpha =\frac{hipotenusa}{catetooposto}=\frac{1}{\sin \alpha }$

• a función chamada cotanxente (abreviada cotan, inda que tamén se pode ver como cotg en outros idiomas, e cot nas fórmulas LaTeX) relaciona as dúas anteriores e é inversa da tanxente: é dicir, é a relación entre o coseno e o seno ou entre a secante e a cosecante. Para facer que o coseno teña valor unitario, faise coincidir co raio, e polo tanto a tanxente é o segmento azul, exterior á circunferencia, é dicir, a cotanxente terá o valor do cateto contiguo cando o cateto oposto vale a unidade:

$\cot \alpha =\frac{\cos \alpha }{\sin \alpha }=\frac{\frac{catetoadxacente}{hipotenusa}}{\frac{catetooposto}{hipotenusa}}=\frac{\sec \alpha }{\csc \alpha }=\frac{catetoadxacente}{catetooposto}$

Funcións inversas para a composición de funcións (funcións arco)

Para unha circunferencia de raio 1, arcsin e arccos son as lonxitudes dos arcos reais determinadas polas cantidades en cuestión.

O concepto de inversión nestas funcións opostas non consiste no valor matematicamente inversamente proporcional segundo a matemática (inverso multiplicativo), senón no concepto contrario ou función inversa.

O seu argumento son números reais e o seu resultado son os ángulos ou arcos (en radiáns). Debido a isto as funcións teñen por nome a denominación da función directa antecedido do prefixo arco-. Así, existen seis funcións inversas: arcoseno ($\arcsin$), arcocoseno ($\arccos$), arcotanxente ($\arctan$), arcosecante ($\mathrm{arcsec}$), arcocosecante ($\mathrm{arccsc}$) e arcocotanxente ($\mathrm{arccot}$).

Así, cando nunha fómula matemática lemos ${\sin }^{-1}x$, débese interpretar como $\arcsin x$. Para o inverso multiplicativo $\frac{1}{\sin x}$ usaríase $(\sin x{)}^{-1}$.

Teorema fundamental dos triángulos

Enúnciase como: a suma dos ángulos dun triángulo suma 180º, medida que equivale a π radiáns. Para outros polígonos regulares se pode calcular (e tamén o ángulo interior de cada un dos seus vértices) mediante o seguinte construto baseado neste teorema (as cores son referidas ás da figura):

Cálculo do ángulo dun polígono regular

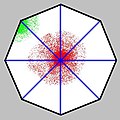
• Se un polígono ten n lados e se busca o centro de simetría radial, se pode unir os n vértices mediante n segmentos (en azul);
• Isto produce n triángulos interiores que terán $n180^{\circ }$
• Tendo en conta que a suma dos ángulos que rodean ó centro de simetría é 360º (en vermello), o resto dos ángulos miden en conxunto:

$n180^{\circ }-360^{\circ }=(n-2)180^{\circ }$

• Como o polígono ten n vértices, a cada un corresponderalle:

$\frac{(n-2)180^{\circ }}{n}=\frac{n-2}{n}180^{\circ }=(1-\frac{2}{n})180^{\circ }$ (en verde)

• Este valor a medida que se vai aumentando (o seu límite cando n tende a infinito) equivale a 180º, que é o valor da tanxente da circunferencia (o polígono de infinitos lados).

Teorema fundamental da trigonometría

Este teorema baséase no teorema de Pitágoras e relaciona o seno dun ángulo co seu coseno. A súa demostración é moi doada partindo do dito por Pitágoras e dividíndoo entre o cadrado da hipotenusa ($catet{o}_O$ é o cateto oposto e $catet{o}_C$ é o cateto contiguo):

$\begin{array}{cccc}{\text{cateto}}_O^2+{\text{cateto}}_C^2& =& {\text{hipotenusa}}^2& \Rightarrow \\ \frac{{\text{cateto}}_O^2}{{\text{hipotenusa}}^2}+\frac{{\text{cateto}}_C^2}{{\text{hipotenusa}}^2}& =& \frac{{\text{hipotenusa}}^2}{{\text{hipotenusa}}^2}& \Rightarrow \\ {\left(\frac{{\text{cateto}}_O}{\text{hipotenusa}}\right)}^2+{\left(\frac{{\text{cateto}}_C}{\text{hipotenusa}}\right)}^2& =& 1& \Rightarrow \\ {\cos }^2\alpha +{\sin }^2\alpha & =& 1\end{array}$

Relacións trigonométricas

Modelo:Ap Existe unha relación entre as funcións trigonométricas de varios ángulos (restados ou sumados) e as funcións de cada un dos sumandos ou restandos individualmente. Disto dedúcese a relación entre as funcións dun ángulo e o do seu dobre (facendo a suma de si mesmo). Tamén hai unha equivalencia entre a función dun ángulo e o da súa metade.

Funcións trigonométricas dunha diferenza	$\sin (\alpha -\beta )=\sin \alpha \cos \beta -\cos \alpha \sin \beta$	$\cos (\alpha -\beta )=\cos \alpha \cos \beta +\sin \alpha \sin \beta$	$\tan (\alpha -\beta )=\frac{\tan \alpha -\tan \beta }{1+\tan \alpha \tan \beta }$
Funcións trigonométricas dunha suma	$\sin (\alpha +\beta )=\sin \alpha \cos \beta +\cos \alpha \sin \beta$	$\cos (\alpha +\beta )=\cos \alpha \cos \beta -\sin \alpha \sin \beta$	$\tan (\alpha +\beta )=\frac{\tan \alpha +\tan \beta }{1-\tan \alpha \tan \beta }$
Funcións trigonométricas do ángulo dobre (deducibles das anteriores)	$\sin (2\alpha )=2\sin \alpha \cos \alpha$	$\cos (2\alpha )={\cos }^2\alpha -{\sin }^2\alpha$	$\tan (2\alpha )=\frac{2\tan \beta }{1-{\tan }^2\alpha }$
Funcións trigonométricas do ángulo metade	$\sin \left(\frac{1}{2}\alpha \right)=\sqrt{\frac{1-\cos \alpha }{2}}$	$\cos \left(\frac{1}{2}\alpha \right)=\sqrt{\frac{1+\cos \alpha }{2}}$	$\tan \left(\frac{1}{2}\alpha \right)=\frac{\sin \left(\frac{1}{2}\alpha \right)}{\cos \left(\frac{1}{2}\alpha \right)}=\sqrt{\frac{1-\cos \alpha }{1+\cos \alpha }}$
Suma de funcións trigonométricas	$\sin \alpha +\sin \beta =2\sin \left(\frac{\alpha +\beta }{2}\right)\cos \left(\frac{\alpha -\beta }{2}\right)$	$\cos \alpha +\cos \beta =2\sin \left(\frac{\alpha +\beta }{2}\right)\cos \left(\frac{\alpha -\beta }{2}\right)$
Resta de funcións trigonométricas	$\sin \alpha -\sin \beta =2\sin \left(\frac{\alpha +\beta }{2}\right)\cos \left(\frac{\alpha -\beta }{2}\right)$	$\cos \alpha -\cos \beta =2\sin \left(\frac{\alpha +\beta }{2}\right)\cos \left(\frac{\alpha -\beta }{2}\right)$

Para coñecer o valor da derivada das funcións trigonométricas (directas, inversas e opostas) v. derivada.