Cuadrilátero

Imaxe dun cuadrilátero.

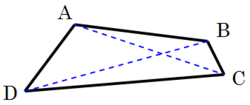
En xeometría euclidiana, un cuadrilátero, cuadrángulo ou tetrágono é un polígono de catro lados e catro vértices.

Proposicións

• Os cuadriláteros teñen dúas diagonais.
• As diagonais dun cuadrilátero córtanse nun punto interior, se e só se é convexo.

• A suma das medidas dos ángulos dun cuadrilátero $ABCD$ convexo es 360º ou 2π radiáns.

$\mathrm{\angle }A+\mathrm{\angle }B+\mathrm{\angle }C+\mathrm{\angle }D=360^{\circ }$

• Se un cuadrilátero está inscrito nunha circunferencia, a suma da medida dos seus ángulos opostos é igual a 180º.
• Sexa ABCD un cuadrilátero inscrito nunha circunferencia de diámetro $AB$, entón as proxeccións dos lados AD e BC sobre a recta CD son iguais.
• A área dun cuadrilátero inscrito obtense coa fórmula $A=\sqrt{(p-a)(p-b)(p-c)(p-d)}$ onde a, b, c, d son os lados e p é o semiperímetro.
• Se se unen con catro segmentos os puntos medios de todos os lados dun cuadrilátero, entón eses segmentos forman un paralelogramo.
• Se un cuadrilátero está circunscrito entón a suma dos seus lados opostos son iguais. $AB+CD=BC+DA$.
• Para un cuadrilátero convexo cúmprese que $a^2+b^2+c^2+d^2=d_1^2+d_2^2+4m^2$ onde $a,b,c,d$ son os lados; $d_1,d_2$, as diagonais e m, a lonxitude do segmento que une os puntos medios das diagonais.
• Tamén se verifica: $d_1^2+d_2^2=m_1^2+m_2^2$ onde $d_1,d_2$ son as diagonais e $m_1,m_2$ son os segmentos, que unen os puntos medios de lados opostos, chamados simedianas.

Elementos dun cuadrilátero

Os elementos dun cuadrilátero son:

• 4 vértices: puntos de intersección dos lados que conforman o cuadrilátero.
• 4 lados: segmentos que unen os vértices contiguos.
• 2 diagonais: segmentos con extremos que son dous vértices non contiguos.
• 4 ángulos interiores: o determinado por dous lados contiguos.
• 4 ángulos exteriores: o determinado pola prolongación dun dos lados sobre un vértice e o contiguo no mesmo vértice.
• Un incentro, centro da circunferencia inscrita.

Clasificación dos cuadriláteros

• Cóncavo. Un dos seus ángulos é maior de 180 graos.
• Convexo. Todos os seus ángulos internos son menores de 180 graos.

Clasificación dos cuadriláteros convexos

• Paralelogramo: os lados son paralelos dous a dous. Polo tanto, os lados opostos teñen a mesma lonxitude, e os ángulos opostos teñen a mesma amplitude. Entre os paralelogramos distinguimos:
  • Cadrado ten catro lados iguais e catro ángulos iguais, que son rectos. Sendo equilateral e equiangular, é un cuadrilátero regular.
  • Rectángulo ten catro ángulos rectos.
  • Rombo cun par de lados consecutivos iguales. Como os lados opostos a estes tamén son os mesmos, o rombo ten catro lados iguais.
  • Romboide cando non ten ángulo recto, nin ten ningún par de lados iguais consecutivos.
• Trapecio: té exactamente un par de lados paralelos (os outros non o son, porque se non sería un paralelogramo). Existen os distintos tipos de trapecios:
  • Rectángulo, cando ten un lado perpendicular aos lados paralelos.
  • Isóscele, cando os lados non paralelos son iguais.
  • Escaleno, cando ningún dos lados é igual a ningún dos outros tres.
  • Rectángulo escaleno, é o trapecio escaleno con dous ángulos rectos
• Trapezoide: ningún par de lados paralelos. Entre os trapezoides atópanse:
  • Unirrectángulo, exactamente en ángulo recto.
  • Birrectángulo, con dous ángulos rectos nin máis nin menos.
  • Deltoides asumen a figura de dous triángulos isósceles (lados diferentes no vértice) cunha base común.
• Inscrito ou cíclico, cando os seus vértices están nunha circunferencia e os seus lados son cordas consecutivas.

Fórmulas

Os catro lados dun cuadrilátero: a, b, c, d ;
os catro vértices: A, B, C, D ;
as dúas diagonais: e, f.

• A suma dos ángulos internos é igual a 360°:

$\alpha +\beta +\gamma +\delta =360^{\circ }$

• Se as diagonais son perpendiculares, cúmprese a seguinte relación:

$\theta =90^{\circ }⟺a^2+c^2=b^2+d^2$

• A área dun cuadrilátero pódese calcular mediante calquera destas fórmulas:

$A=\frac{ef\sin \theta }{2}$ $A=\frac{ad\sin \alpha +bc\sin \gamma }{2}=\frac{ab\sin \beta +cd\sin \delta }{2}$ $A=\frac{1}{4}(b^2+d^2-a^2-c^2)\tan \theta$ $A=\frac{1}{4}\sqrt{4e^2{f}^2-{(b^2+d^2-a^2-c^2)}^2}$ $A=\frac{1}{2}\sqrt{|\overrightarrow{e}{|}^2|\overrightarrow{f}{|}^2-(\overrightarrow{e}\cdot \overrightarrow{f}{)}^2}$

$A=\frac{1}{2}ad\cdot \sin \alpha +\frac{1}{4}\sqrt{4b^2{c}^2-(b^2+c^2-a^2-d^2+2ad\cdot \cos \alpha {)}^2}$ (para un cuadrilátero con concavidade en C cambiar o primeiro signo + por -).

Cuadriláteros inscritos

Son aqueles con vértices que están sobre unha circunferencia e os seus lados son cordas. Establécense as seguintes fórmulas, sendo Modelo:Ecuación

Modelo:Ecuación

Teorema de Arquímedes-Faure

Dado o cuadrilátero inscrito de lados a, b, c, d; de diagonais perpendiculares que ao intersecárense determinan os segmentos m, n nun deles e p, q no outro, R o raio da circunferencia circunscrita. En tal caso cúmprense as igualdades: Modelo:Ecuación Modelo:Ecuación

Cuadrilátero circunscrito

Con lados tanxentes a unha circunferencia e os seus vértices son puntos comúns a cada dous lados tanxentes.

Véxase tamén

Outros artigos

• Cuadrilátero cíclico
• Cuadrilátero tanxencial