Media metálica
| Media metálica (proporcións metálicas) | |||
|---|---|---|---|
| N | Proporción | Valor | Nome |
| 0 | Modelo:Sfrac | 1 | |
| 1 | Modelo:Sfrac | 1.618033989Modelo:Efn | Ouro |
| 2 | Modelo:Sfrac | 2.414213562Modelo:Efn | Prata |
| 3 | Modelo:Sfrac | 3.302775638Modelo:Efn | Bronce |
| 4 | Modelo:Sfrac | 4.236067978Modelo:Efn | |
| 5 | Modelo:Sfrac | 5.192582404Modelo:Efn | |
| 6 | Modelo:Sfrac | 6.162277660Modelo:Efn | |
| 7 | Modelo:Sfrac | 7.140054945Modelo:Efn | |
| 8 | Modelo:Sfrac | 8.123105626Modelo:Efn | |
| 9 | Modelo:Sfrac | 9.109772229Modelo:Efn | |
| 10 | Modelo:Sfrac | 10.099019513Modelo:Efn | |
| ⋮ | |||
| n | Modelo:Sfrac | ||
As medias metálicas (ou ratios ou constantes) dos sucesivos números naturais son as fraccións continuas con coeficientes constantes:
A proporción áurea (1.618...) é a media metálica situada entre 1 e 2, mentres que a proporción de prata (2.414...) é a media metálica situada entre 2 e 3. O termo "proporción de bronce" (3.303...), e outros nomes de metais (como cobre ou níquel), empréganse ocasionalmente para denominar as medias metálicas posteriores. [1] [2] Os valores das dez primeiras medias metálicas móstranse na táboa da dereita. [3] [4] Observe que cada media metálica é unha raíz da ecuación cadrática simple: , onde é calquera número natural positivo.
A proporción áurea está conectada co pentágono (primeira diagonal/lado), a proporción de prata está conectada co octógono (segunda diagonal/lado). A proporción áurea está conectada aos números de Fibonacci, a proporción de prata está conectada aos números de Pell, e a proporción de bronce está conectada a Modelo:OEIS.
Así para cada temos as recorrencias lineais de segunda orde:
Fibonacci (ouro): 0, 1, 1, 2, 3, 5, 8, 13 ...
Pell (prata): 0, 1, 2, 5, 12, 29, 70 ...
Modelo:OEIS (bronce): 0, 1, 3, 10, 33, 109 ...
Propiedades
Estas propiedades só son válidas para números enteiros. Para os non enteiros as propiedades son lixeiramente diferentes.
Chamamos á media metálica relacionada coa constante Modelo:Mvar.
Sendo os converxentes da fracción continua temos que
A recorrencia asociada a cada son os denominadores (ou os numeradores excluído o cero) dos converxentes da fracción continua .
Sendo a recorrencia asociada a temos que
Unha relación para a inversa da media metálica
por tanto os inversos das medias metálicas son a parte decimal do número correspondente.
Se descompomos en para enteira Modelo:Mvar e parte fraccional Modelo:Mvar, temos:
- , e resulta
As medias metálicas de n en forma de integral,
En relación a funcións hiperbólicas,
Expresións trigonométricas
| Expresión trigonométrica | ||
|---|---|---|
| N | Fórmula | Polígono regular asociado |
| 1 | pentágono | |
| 2 | octógono | |
| 3 | ||
| 4 | ||
Construción xeométrica
A media metálica para calquera número enteiro dado pódese construír xeométricamente do seguinte xeito. Defínese un triángulo rectángulo con lados e tendo lonxitudes e , respectivamente. A media metálica é simplemente a suma da lonxitude de e a hipotenusa . [5]
Para ,
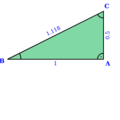
e logo
φ.
Con dá a proporción de prata.
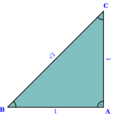
A proporción de bronce con ,

Os argumentos non enteiros ás veces producen triángulos cunha media que é un número enteiro. Un exemplo con , temos

que é simplemente unha versión reducida do triángulo pitagórico 3–4–5.
Notas
Modelo:Reflist Modelo:Notelist
Véxase tamén
Bibliografía
- Stakhov, Alekseĭ Petrovich (2009). The Mathematics of Harmony: From Euclides to Contemporary Mathematics and Computer Science, p. 228, 231.World Scientific.Modelo:ISBN.
Ligazóns externas
- Cristina-Elena Hrețcanu and Mircea Crasmareanu (2013). "Metallic Structures on Riemannian Manifolds", Revista de la Unión Matemática Argentina.
- Rakočević, Miloje M. "Further Generalization of Golden Mean in Relation to Euler's 'Divine' Equation", Arxiv.org.
- ↑ Vera W. de Spinadel (1999). The Family of Metallic Means, Vismath 1(3) from Mathematical Institute of Serbian Academy of Sciences and Arts.
- ↑ Modelo:Cita publicación periódica
- ↑ <templatestyles src="Module:Citation/CS1/styles.css"></templatestyles>Modelo:MathWorld
- ↑ "An Introduction to Continued Fractions: The Silver Means", maths.surrey.ac.uk.
- ↑ Modelo:Cita publicación periódica